Probabilité, v.a défini par récurrence
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aviateur
 par aviateur » 13 Mar 2019, 18:48
par aviateur » 13 Mar 2019, 18:48
tournesol a écrit:@ aviateur
,(0;1),(1;0),(1;1)\})
avec équiprobabilité .
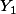
= abscisse ,
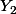
= ordonnée ,
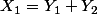
, et
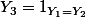
On a
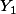
et
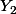
indépendantes mais surtout :
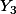
et
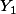
indépendantes ainsi que
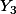
et
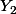
(démo infra)
Or

ne dépend que des valeurs prises par
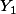
et
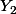 donc l'indépendance de
donc l'indépendance de 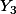 avec
avec  est évidente .
est évidente .Sauf que
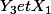
ne sont pas indépendantes.
Pas indépendantes logiquement :
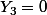
ssi
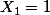
Ni stochastiquement :
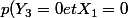=0)
par incompatibilité .
Mais
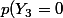=1/2)
et
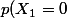=1/4)
infra
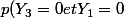=p((1;0))=1/4)
et
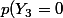 \times p( Y_1=0)=1/2\times 1/2=1/4)
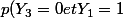=p((0;1))=1/4)
et
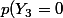 \times p( Y_1=1)=1/2\times 1/2=1/4)
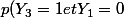=p((0;0))=1/4)
et
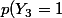 \times p( Y_1=0)=1/2\times 1/2=1/4)
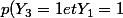=p((1;1))=1/4)
et
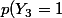 \times p( Y_1=1)=1/2\times 1/2=1/4)
Ce que tu dis en rouge je ne comprends pas.
-
aviateur
 par aviateur » 13 Mar 2019, 19:08
par aviateur » 13 Mar 2019, 19:08
@tournesol
J'ai l'impression que tu extrapoles ce que j'ai dit au niveau de l'indépendance.
En effet si j'ai X, Y et Z mutuellement indépendantes on a alors Z est indépendante de X+Y. Je n'ai rien utilisé de plus.
Si tu enlèves une hypothèse évidemment ça ne marche plus.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 13 Mar 2019, 19:17
par tournesol » 13 Mar 2019, 19:17
Moi non plus (voir mon avant dernier message)
-
aviateur
 par aviateur » 13 Mar 2019, 19:32
par aviateur » 13 Mar 2019, 19:32
Ton avant dernier message les v.a ne sont pas mutuellement indépendantes.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 13 Mar 2019, 19:52
par tournesol » 13 Mar 2019, 19:52
Merci aviateur. Je vais réfléchir à tout cela .
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 13 Mar 2019, 21:23
par tournesol » 13 Mar 2019, 21:23
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
avec équiprobabilité .
= abscisse ,
= ordonnée ,
, et
et
indépendantes mais surtout :
et
indépendantes ainsi que
et
(démo infra)
ne dépend que des valeurs prises par
et
donc l'indépendance de
avec
est évidente .
ne sont pas indépendantes.
ssi
par incompatibilité .
et
et
et
et
et
