Proba
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Elganar
- Membre Naturel
- Messages: 79
- Enregistré le: 08 Avr 2013, 16:24
-
 par Elganar » 21 Avr 2015, 17:16
par Elganar » 21 Avr 2015, 17:16
Bonjour,
Encore un petit problème dans un exo.
Surement les vacances qui font perdre le niveau...
On considère une urne contenant n boules, numérotés de 1 à n. On tire au hasard deux boules dans cette urne avec remise. On note X le plus grand des numéros tirés.Donnez donc P(X=k) avec k variant donc de 1 à n.
--> Selon moi c'est

car il faut déjà tirer la boule k soit
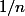
puis une boule au plus égal à k soit

. Mais la somme de toutes ces proba ne fait pas 1...
Auriez-vous une petite aide?
Merci d'avance ^^
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 21 Avr 2015, 17:21
par Sylviel » 21 Avr 2015, 17:21
Bonjour,
tu es parti du principe que la première boule tirée était celle qui réalisait le max...
Ca peut aussi être la seconde boule ! (attention au cas d'égalité)
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Elganar
- Membre Naturel
- Messages: 79
- Enregistré le: 08 Avr 2013, 16:24
-
 par Elganar » 21 Avr 2015, 17:30
par Elganar » 21 Avr 2015, 17:30
Je ne vois pas comment faire dans ce cas.
J'ai l'impression que ça revient au même en fait. Pour obtenir k, il faut:
Premier tirage:
Tirer k ou moins
Second tirage:
Si k est tirer, alors tirer k ou moins.
Si k n'est pas tiré mais moins, alors tirer k.
/n^2)
/n^2)
Je dirais donc ça ^^
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 21 Avr 2015, 17:34
par Sylviel » 21 Avr 2015, 17:34
Ce n'est pas très clair. Appelons U1 le premier tirage et U2 le second tirage. On a
{X = k} = {U1 = k, U2 es-tu d'accord ?
Tu n'as plus qu'à calculer la probabilité de chaque évènement et faire la somme (pourquoi ?).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Elganar
- Membre Naturel
- Messages: 79
- Enregistré le: 08 Avr 2013, 16:24
-
 par Elganar » 21 Avr 2015, 17:37
par Elganar » 21 Avr 2015, 17:37
Voilà merci le résultat est le même.
En fait dans mon message je pensais pas trouver en l'écrivant et au final c'est bon ^^
Merci bien !!
-
Elganar
- Membre Naturel
- Messages: 79
- Enregistré le: 08 Avr 2013, 16:24
-
 par Elganar » 21 Avr 2015, 18:02
par Elganar » 21 Avr 2015, 18:02
Montrez que E(X)= (n+1))/6n)
Dans l'énoncé il y a la formule de la somme des
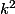
Je trouve
(2n)/6n)
-
Elganar
- Membre Naturel
- Messages: 79
- Enregistré le: 08 Avr 2013, 16:24
-
 par Elganar » 21 Avr 2015, 18:56
par Elganar » 21 Avr 2015, 18:56
Si je trouve mais pas exactement
(n+1)/6n)
Je sais pas où est le problème...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 21 Avr 2015, 19:09
par zygomatique » 21 Avr 2015, 19:09
salut
et que vaut P(X = k) ? donc kP(X = k) ? donc leur somme ?
doit-on faire les calculs à ta place ou nous montres-tu ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Elganar
- Membre Naturel
- Messages: 79
- Enregistré le: 08 Avr 2013, 16:24
-
 par Elganar » 21 Avr 2015, 19:12
par Elganar » 21 Avr 2015, 19:12
J'ai fais les calculs, je sais pas comment on fait une somme avec TEX,
mais je trouve:
(2n+1)-3n(n+1)/6n)
De degré 3 en haut du coup y'a un problème...
-
Elganar
- Membre Naturel
- Messages: 79
- Enregistré le: 08 Avr 2013, 16:24
-
 par Elganar » 22 Avr 2015, 09:33
par Elganar » 22 Avr 2015, 09:33
Quelqu'un arrive t-il au résultat?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 22 Avr 2015, 10:04
par Ben314 » 22 Avr 2015, 10:04
Salut,
Déjà, pour trouver la loi de X, j'aurais fait un peu différemment :
On a X<=k ssi les deux boules tirées sont <=k donc
=\big(\frac{k}{n}\big)^2)
puis
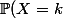={\mathbb P}(X\leq k)-{\mathbb P}(X\leq k-1)=\big(\frac{k}{n}\big)^2-\big(\frac{k-1}{n}\big)^2=\frac{2k-1}{n^2})
(l'intérêt de cette méthode, c'est que si on tirait 15 boules, elle s'appliquerait tout pareil...)
Ensuite
<br /> = \sum_{k=1}^nk\times{\mathbb P}(X=k)<br /> = \frac{1}{n^2}\sum_{k=1}^n(2k^2-k)<br /> = \frac{1}{n^2}\Big(2\sum_{k=1}^nk^2-\sum_{k=1}^nk\Big)<br /> = \frac{1}{n^2}\Big(2\frac{n(n+1)(2n+1)}{6}-\frac{n(n+1)}{2}\Big)<br /> = \frac{(n+1)(4n-3)}{6n})
On vérifie que, pour n=1, ça fait 1, que pour n=2, ça fait 7/4=1.75 et que, lorsque n devient assez grand, c'est environ 2n/3 (cohérent).
EDIT : Pour le MimeTeX, regarde là
http://www.maths-forum.com/ecrire-belles-formules-mathematiques-balises-tex-70548.phpQui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Elganar
- Membre Naturel
- Messages: 79
- Enregistré le: 08 Avr 2013, 16:24
-
 par Elganar » 22 Avr 2015, 10:35
par Elganar » 22 Avr 2015, 10:35
J'avais oublié le ^2... Merci bien ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités
