Proba / Stat

[jujudu597]

Bonjour,

Un exercice me pose problème donc j'aimerais votre aide.

On considère n fonctions définies sur le même ensemble et à valeurs dans . Pour i allant de 1 à n, on note;



Exprimer à l'aide des les ensembles:



et




J'ai pensé à l'intersection et l'union des Ai mais on a pas de max qui intervient.

Jspr que vous pouriez m'aider. Merci d'avance

[Robic]

Pour ce genre d'exercice où, au début, je ne vois pas la réponse, je procède toujours en "traduisant" l'énoncé.

Ici on demande de déterminer B' (oui, je réponds pour le deuxième, que je l'appelle B' vu qu'il y a déjà un B). Pour ça, il faut trouver une condition pour qu'un appartienne à B'. C'est comme ça qu'on définit un ensemble, voir par exemple la façon dont on défini : l'ensemble des tels que .

Ici il faut donc trouver une condition, et ensuite on dira que c'est l'ensemble des tels que (cette condition).

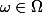
Bref, soit . On veut que .

1ère étape : que signifie ?

(je ne fais que recopier la définition).

2ème étape : que signifie ? Ça signifie que si on fait la liste , , , , etc. alors le plus petit d'entre eux est positif.

Donc ils sont tous positifs (vu que les autres sont plus grands que le plus petit d'entre eux).

Donc :



3ème étape : que signifie ? Ça signifie que pour tout i, est dans l'ensemble :



4ème étape : que signifie ? Si un élément est dans tous les ensembles, il est dans leur intersection. Donc :



et il reste à conclure (si truc est équivalent à machin, c'est que truc = machin). Pour B, c'est similaire.

[jujudu597]

Merci beaucoup pour votre message. Il m'a été d'une très grande aide!