Proba: récursive en 1/n
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
fonfred
- Membre Naturel
- Messages: 12
- Enregistré le: 10 Fév 2007, 17:16
-
 par fonfred » 05 Fév 2013, 16:08
par fonfred » 05 Fév 2013, 16:08
Bonjour,
je me pose un petit problème, je ne sais pas s'il y a une solution, ni à quel programme scolaire il peut se rattacher.
Soit
)
la probabilité qu'un événement arrive à l'instant

(entier)
Si il y a eu un événement à
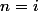
alors
= \frac{1}{\Gamma*(j-i)})
avec

.
Je cherche donc à écrire
)
en fonction de

et

avec comme hypothèse
=1)
.
une relation, si elle existe,
)
=>
)
serait suffisante.
J'espère avoir été clair et qu'il ne manque pas de données à mon problème.
Merci pour votre aide.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 05 Fév 2013, 16:31
par fatal_error » 05 Fév 2013, 16:31
slt,
c'est quoi la difference entre
Gamma <1, j>
et
Gamma(j-i)
?
est-ce que Gamma represente la fonction gamma? et si oui, ca veut dire quoi Gamma <1,j>
la vie est une fête

-
fonfred
- Membre Naturel
- Messages: 12
- Enregistré le: 10 Fév 2007, 17:16
-
 par fonfred » 05 Fév 2013, 16:33
par fonfred » 05 Fév 2013, 16:33
fatal_error a écrit:slt,
c'est quoi la difference entre
Gamma
et
Gamma(j-i)
?
est-ce que Gamma represente la fonction gamma? et si oui, ca veut dire quoi Gamma
Gamma est une constante inférieur à 1.
dans l'équation j'ai Gamma * (j-i).
les sont des inférieur et supérieur et non pas la notation bra ket par ex..
Merci

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 05 Fév 2013, 20:20
par fatal_error » 05 Fév 2013, 20:20
j'appele C gamma, puisque c'est une constante (et que c'est moins chiant à écrire)
on a
}{u(j-1)} = \frac{ \frac{1}{C\times (j-i)} }{ \frac{1}{C\times (j-1-i)}} = \frac{j-1-i}{j-i}=1 - \frac{1}{j-i})
Or

donc

et

donc

et donc
 \lt u(j-1))
ce qui est le contraire de ce que tu as attends.
Note: u(n) étant une probabilité, je l'ai considérée comme positive.
idem :

Note2:
Je cherche donc à écrire u(n) en fonction de n et \Gamma
c'est déjà le cas, t'as juste à remplacer j par n!
la vie est une fête

-
fonfred
- Membre Naturel
- Messages: 12
- Enregistré le: 10 Fév 2007, 17:16
-
 par fonfred » 05 Fév 2013, 20:44
par fonfred » 05 Fév 2013, 20:44
Merci, je prends un peu le temps de comprendre et je reviens.
-
fonfred
- Membre Naturel
- Messages: 12
- Enregistré le: 10 Fév 2007, 17:16
-
 par fonfred » 05 Fév 2013, 21:05
par fonfred » 05 Fév 2013, 21:05
fonfred a écrit:Merci, je prends un peu le temps de comprendre et je reviens.
me revoilà déjà
A mon avis je me suis mal exprimé:
pour moi:
=\frac{1}{c})
=(1-\frac{1}{c})\frac{1}{c}+\frac{1}{c^2})
=(1-\frac{1}{c})(1-\frac{1}{2c})\frac{1}{3c}+(1-\frac{1}{c})\frac{1}{2c}\frac{1}{c}+\frac{1}{c}(1-\frac{1}{c})\frac{1}{2c}+\frac{1}{c^3})
Je ne sais pas pourquoi mes équations sont toutes de travers :triste:
Par exemple pour u(3) je regarde les cas [0 0 1] , [0 1 1], [1 0 1] et [1 1 1]. pour le dernier c'est simple avoir un événement en 1 arrive avec un propa de 1/c vu qu'il est arrivé la proba est de nouveau 1/c pour u(2) vu qu'il arrive aussi la proba est encore de 1/c pour u(3).
Je me plante quelques part?
merci
-
fonfred
- Membre Naturel
- Messages: 12
- Enregistré le: 10 Fév 2007, 17:16
-
 par fonfred » 06 Fév 2013, 13:56
par fonfred » 06 Fév 2013, 13:56
Vous pensez qu'il n'y a pas de solution ?

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 06 Fév 2013, 14:06
par fatal_error » 06 Fév 2013, 14:06
je comprends pas ce que tu essaies de faire.
Par exemple pour u(3) je regarde les cas [0 0 1] , [0 1 1], [1 0 1] et [1 1 1]
je sais pas ce que tes crochets representent.
Je sais meme pas comment tu calcules tes u(n).
Est-ce que tu connais la relation de reccurrence u(n) en fonction de u(n-1)?
sinon qu-est-ce que ca repsente u(n)
pe peux-tu fournir un schema?
la vie est une fête

-
fonfred
- Membre Naturel
- Messages: 12
- Enregistré le: 10 Fév 2007, 17:16
-
 par fonfred » 06 Fév 2013, 14:28
par fonfred » 06 Fév 2013, 14:28
J'ai un phénomène physique piloté par une horloge de période "1". Au départ n=0 je charge mon système. Celui-ci sera "stressé" à chaque coup d'horloge n=1,2,...inf . La probabilité qu'il réponde (événement positif) et U(n)=1/c*n (formule de mon premier message). Si il répond positif alors il est de nouveau chargé et on revient à l'état initial.
Bref à partir de n=0 il est facile de calculer la probabilité d'avoir un 1er événement pour n=k => 1/c*k.
Mais si je prend n=3 par exemple la probabilité d'y voir une événement positif sera la somme de
[0 0 1] j'ai rien eu en n=1 rien en n=2 l'événement en n=3 ou [1 0 1] un événement en n=1 rien en n=2 ainsi de suite.
Suis-je plus lcair.
Merci

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 06 Fév 2013, 19:46
par fatal_error » 06 Fév 2013, 19:46
confirmes tu qu'en n=3, les solutions sont
[0 0 1]
[0 1 1]
[1 0 1]
[1 1 1]
?
la vie est une fête

-
fonfred
- Membre Naturel
- Messages: 12
- Enregistré le: 10 Fév 2007, 17:16
-
 par fonfred » 07 Fév 2013, 15:49
par fonfred » 07 Fév 2013, 15:49
Oui c'est le cas. c'est bien ces 4 solutions, pour n=4 il y aura 8 solutions etc...
Désolé pour le temps mis à répondre.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 07 Fév 2013, 19:24
par fatal_error » 07 Fév 2013, 19:24
alors,
Je note Xn le nieme chiffre tiré (qui vaut 1 ou 0)
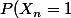=\bigsum_{j=0}^{n-1}P(\text{precedent 1 en position j})\times P(\text{que des 0 de j+1 a n-1})\times P(\text{nb 0+1 coups}))
On commence avec j=0, signifiant que on commence par un zéro
ce qui donne
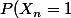=\bigsum_{j=0}^{n-1} P(Xj=1)\times \bigprod_{k=1}^{n-1-j}(1-p(k)) \times p(n-j))
avec
=\frac{1}{ck})
en particulier aux valeurs limites de j on a
j=0: P(X-1=1) = 1
j=n-1: produit de k=1 à 0...ce qui est pas bon.
On réécrit donc
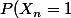=[ \bigsum_{j=0}^{n-2} P(Xj=1)\times \bigprod_{k=1}^{n-1-j}(1-p(k)) \times p(n-j) ] +P(X_{n-1}=1)p(1))
Je suis pas convaincu qu'on explicite facilement P(X_n=1) en fonction de c et n.
Il faudrait arriver à étudier le signe de P(Xn=1)-P(Xn-1=1)
la vie est une fête

-
fonfred
- Membre Naturel
- Messages: 12
- Enregistré le: 10 Fév 2007, 17:16
-
 par fonfred » 08 Fév 2013, 11:02
par fonfred » 08 Fév 2013, 11:02
Merci, j'essaie de comprendre, et je reviens...
-
fonfred
- Membre Naturel
- Messages: 12
- Enregistré le: 10 Fév 2007, 17:16
-
 par fonfred » 08 Fév 2013, 17:04
par fonfred » 08 Fév 2013, 17:04
Super c'est bien ce que je cherche !
On remarque que [0 1 1] = [1 0 1] ou [0 0 1 1] = [1 0 0 1] et [0 1 1 1] = [1 0 1 1] = [ 1 1 0 1].
Dans un souci calculatoire ça serait possible de les faire apparaitre dans l'équation ?
Pour moi: P(Xn=1)-P(Xn-1=1) < 0 sinon physiquement ça n'irait pas mon truc.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
