Proba ; esperance et ecart type

[juju78]

bonjour,

La durée mesurée en minutes de séjour d'un client dans un magasin est une variable aléatoire X distribuée selon une loi exponentielle de paramètre 10, c'est à dire avec la densité de proba suivante:

f(x)=

si x => 0
0 sinon

On me demande de calculer l'esperance
soit
Après un calcul àl'aide de la méthode de l'intégration par parties je trouve

E(x)=10

On me demande alors de calculer soit
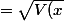or V(x)= E(x²) - [E(x)]²

Je commence donc par calculer
E(x²)=

Mais au lieu de refaire un long calcul ennuyeux a l'aide de la méthode d'intégration par parties il n'y a pas un moyen plus efficace pr le savoir?

[juju78]

a ok c'est parce qu'en fait je rattrape des exos, et je n'ai pas de cours "fixe"donc c''est tjrs bon à savoir lol, merci :)

On me demande ensuite:

Calculez la probabilité que la durée X dépasse 30MN

on doit calculer alors P(X>30)

soit 1-P(X<30)
Mais je dois me rapporter a quelle loi pour le calcul? comment faire? est ce une loi de Poisson, loi normale?

[juju78]

J'ai trouvé sur wikipédia que pour la loi exponentielle on avait:


donc ici on a



?