Proba/Analyse combinatoire

[cpwjuz]

Bonjour,
Est ce que quelqu'un pourrait me dire comment résoudre les questions 2 et 3 sans devoir tout calculé à la main s'il vous plaît, puisque cela donne un arbre très dense, et devoir additionner et multiplier chaque proba semble peu judicieux:
Un sac contient 6 boules qui se répartissent en : - 1 boule verte - 2 boules blanches - 3 boules rouges
On tire 3 boules (sans remise) on demande la probabilité pour que les 3 boules soient :
1. de la même couleur
2. de 2 couleurs différentes
3. de couleurs différentes

[Vassillia]

Bonjour,
Peux-tu nous dire comment tu as résolu la question 1 ?

Dans l'idéal, il faut calculer le nombre de sous-ensemble de 3 boules que l'on peut faire à partir de 6 boules ce qui donne le nombre de cas total. Il faut aussi calculer le nombre de sous-ensemble de 3 boules que l'on peut faire à partir de 3 boules rouges ce qui donne le nombre de cas favorables.

Et bien c'est pareil pour les questions suivantes, essaye de compter le nombre de sous-ensemble favorables.
Par exemple pour 3 couleurs différentes, il te faut combien de boules vertes parmi combien de boules vertes possibles ? même chose pour les boules rouges ? et les boules blanches ?

On verra 2 couleurs différentes à la fin si tu le veux bien

[cpwjuz]

Pour la question 1:
3/6*2/5*1/4 = 1/20
car la quantité de boules diminue.

C'est un arrangement sans rép donc:
6! / 3!= 120 possibilités de triplets.

Pour la question 3: il me faut 1 verte parmi 1, 1 blanche parmi 2 et 1 rouge parmi 3 donc:
1!/1! + 2!/1! + 3!/1! = 9
La probabilité qu'on ait 3 boules de couleurs différentes est donc de 9/120 ?

[Vassillia]

Attention, c'est plutot une combinaison comme l'ordre ne compte pas donc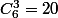
Tu as la bonne réponse pour la question 1/ et on peut aussi la corriger comme

Il y a le même problème pour la question 3/, il faut utiliser des combinaisons mais surtout pourquoi additionner ?
Pour n'importe quel choix de boule verte, on peut choisir n'importe quelle boule blanche...

[cpwjuz]

Je t'avouerai que j'ai additionné un peu au hasard.
Donc avec des combinaisons la 3) donne;
C(1 parmi 1)= 1
C (1 parmi 2)=2
C(1 parmi 3)= 3
Mais maintenant je ne vois pas quoi faire ?

[Vassillia]

Si je rale quand tu additionnes, c'est un indice mais pour savoir quoi faire d'autre mais pour le comprendre essaye d'imaginer:
Je choisis la boule seule
--Je choisis la première des 2 boules
----Je choisis la première des 3 boules (et c'est fini)
----Je choisis la deuxième des 3 boules (et c'est fini)
----Je choisis la troisième des 3 boules (et c'est fini)
--Je choisi la deuxième des 2 boules
---- (et c'est fini)
---- (et c'est fini)
---- (et c'est fini)
On peut construire un arbre en quelque sorte qui va mener à combien de branche donc il faut faire quoi comme opération ?

[cpwjuz]

L'arbre devrait donner 20 branches et donc il faut multiplier les proba entre elles ?
Et donc (1*2*3)/20= 6/20 ?

[Vassillia]

Et bien voilà
Bon, il ne te reste plus que la question 2/
Si tu es très courageux tu peux faire cas par cas (c'est à dire 1 verte + 2 blanche, 1 verte + 2 rouges, 1 blanche + 2 rouges ...) et je conseille de le faire pour l'entrainement
Si tu es plus malin, tu peux te demander que devrait valoir la somme des probas des questions 1/ 2/ et 3/ c'est un peu pour ça que je l'ai gardé pour la fin

[cpwjuz]

Ok merci beaucoup !!!

La somme est de 1 donc, pour la question 2 la réponse est:
1-(6/20)-1/20= 13/20