salut;
j'ai un probleme de demonstration concernon la relation suivante:
qel que soit m,n,p dans l'ensemble N en a :
(m+n)+p = m+(n+p)
seulement en partant de : (m+n)+1 = m+(n+1)
moi j'ai mis :
(m+n)+1 = (m+n-n)+(1+n)
je voudrai savoir si j'ai le droit de partir de la ????? :help:
Prob de demonstration elementaire
9 messages
- Page 1 sur 1
Mr Ashe a écrit:salut;
j'ai un probleme de demonstration concernon la relation suivante:
qel que soit m,n,p dans l'ensemble N en a :
(m+n)+p = m+(n+p)
seulement en partant de : (m+n)+1 = m+(n+1)
moi j'ai mis :
(m+n)+1 = (m+n-n)+(1+n)
je voudrai savoir si j'ai le droit de partir de la ????? :help:
Bonsoir,
Quelles sont l'hypothéses de départ sur l'addition.
La différence n'est pas définie sur N (les naturels), mais sur Z (les relatifs).
bonjour,
on pose (successeur de x)
(successeur de x)
on sait par hypothèse que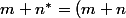^*)
on va montrer par récurrence sur p
: \qquad \forall n,m \qquad (m+n)+p=m+(n+p))
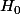 est vraie.
est vraie.
on suppose et on démontre
et on démontre 
------------------------------------------------------------
regardons ce que ça donne sur un exemple:
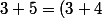^*=7^*)
pour définir 3+5, il faut connaitre le successeur de 3+4.
pour définir "3+5", il faut connaitre le successeur de "3+4".
on écrit des guillemets.
A mon avis, on peut avoir une idée des axiomes de
ainsi:
les entiers sont des objets sans signification particulière, en fait ,une
"occupation mémoire" dans un ordinateur.
on programme en C ou C++
la donnée de la fonction de succession
signifie que ,situé à l'emplacement mémoire qui contient l'objet "n",
on dispose d'un unique "pointeur adresse mémoire" qui pointe , par définition , sur l'objet "n+1".
l'entier "n" peut donc être un article de journal et l'entier "n+1" la photo
d'un coucher de soleil.
Le problème, dans la définition de 3+5, est de connaitre l'emplacement mémoire de l'objet "3+4" puis de chainer,par pointeur, sur son successeur:
on parcourt en fait la liste chainée:
"3+0"->"3+1"->"3+2"->"3+3"->"3+4"->"3+5"
en sachant que 3+0=3
que devient l'associativité ?
exemple: (3+1)+2=3+(1+2)
à gauche, on a ,comme point d'entrée, l'objet "3".
on chaine sur son successeur,l'objet "3+1"
puis on chaine deux fois , en chainage avant, pour obtenir (3+1)+2
bizarre ? il faut des "méta-entiers", dans un compteur de boucle
du programme,pour accéder à nos entiers de Péano. On se mord la queue. :doh:
Le plus raisonnable,c'est de dire, suivant en cela H.Poincaré, que toute définition de est autoréférente et de se ranger à l'avis de Dedekind:
est autoréférente et de se ranger à l'avis de Dedekind:
"en maths, Dieu a inventé les nombres et l'homme (ou la femme) le reste" :we:
à droite, pour obtenir, 3+(1+2), on remonte dans les antécédents de l'objet "3+(1+2)" par chainage arrière sur "3+1" puis, on redescend, par chainage avant, dans la liste de (3+1)+2.
:mur:
on pose
on sait par hypothèse que
on va montrer par récurrence sur p
on suppose
------------------------------------------------------------
regardons ce que ça donne sur un exemple:
pour définir 3+5, il faut connaitre le successeur de 3+4.
pour définir "3+5", il faut connaitre le successeur de "3+4".
on écrit des guillemets.
A mon avis, on peut avoir une idée des axiomes de
ainsi:
les entiers sont des objets sans signification particulière, en fait ,une
"occupation mémoire" dans un ordinateur.
on programme en C ou C++
la donnée de la fonction de succession
signifie que ,situé à l'emplacement mémoire qui contient l'objet "n",
on dispose d'un unique "pointeur adresse mémoire" qui pointe , par définition , sur l'objet "n+1".
l'entier "n" peut donc être un article de journal et l'entier "n+1" la photo
d'un coucher de soleil.
Le problème, dans la définition de 3+5, est de connaitre l'emplacement mémoire de l'objet "3+4" puis de chainer,par pointeur, sur son successeur:
on parcourt en fait la liste chainée:
"3+0"->"3+1"->"3+2"->"3+3"->"3+4"->"3+5"
en sachant que 3+0=3
que devient l'associativité ?
exemple: (3+1)+2=3+(1+2)
à gauche, on a ,comme point d'entrée, l'objet "3".
on chaine sur son successeur,l'objet "3+1"
puis on chaine deux fois , en chainage avant, pour obtenir (3+1)+2
bizarre ? il faut des "méta-entiers", dans un compteur de boucle
du programme,pour accéder à nos entiers de Péano. On se mord la queue. :doh:
Le plus raisonnable,c'est de dire, suivant en cela H.Poincaré, que toute définition de
"en maths, Dieu a inventé les nombres et l'homme (ou la femme) le reste" :we:
à droite, pour obtenir, 3+(1+2), on remonte dans les antécédents de l'objet "3+(1+2)" par chainage arrière sur "3+1" puis, on redescend, par chainage avant, dans la liste de (3+1)+2.
:mur:
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
