Principe de récurrence

[Canehan]

Bonjour, j'ai un exercice à faire et je suis bloqué.
C'est un exercice avec des factoriel et le principe de récurrence. Voici l'énoncé:

"Démontrer par récurrence la propriété suivante: n>n^2 ( à partir d'un entier n0 (à déterminer avec soin) ou la lettre n désigne un entier naturel, et où la notation n! est définie par:
0!=1 ; !=1 ; et si n>1, n!=n (n-1)(n-2)….2*1"
J'ai avancé ainsi:
a) Soit la propriété P(n): n!=n(n-1)(n-2)...2*1
b) Initialisation: Pour n=2 montrer 2!=2*1
2! = 2
2*1=2
Les deux résultats sont égaux onc la propriété est vraie au rang 2.
(J'ai choisi 2 car il ne me semblaitpas que la prorpiété etait vraie au rang 0 ou au rang 1, ce qui s'explique par le fait qu'il est souligné "qu'il faut choisir avec soin" n0)
c) Hérédité: Je suppose que la ropriété est vraie à un certain rang n et je chercher à montrer qu'elle est vraie au rang n+1.

Je suppose que n!=n(n-1)(n-2)...2*1 (hypothèse de récurrence)

Je cherche n+1 à monter que:
n+1! = (n+1) (n+1-1)(n+1-2)...2*1
= (n+1)(n)(n-1)...2*1


n!= 1+2+6+24+120+...+n+(n+1)


n! + (n+1)
= n(n-1)(n-2)...2*1+(n+1)
et à partir d'ici je ne sais plus comment avancer, est ce que cela s'explique par une erreur précédente ? je n'ai jamais eu affaire à des factoriels avant cette exercice (pas même en cours) ce qui je pense ne me facilite pas la tâche. Merci de votre attention et de vos réponses potentielles.

[lyceen95]

Il y a plein de truc qui ne vont pas. Disons même que rien ne va.

Déjà, au moment de recopier l'énoncé, il y a une erreur.
Dans l'énoncé, tu dis qu'il faudrait montrer la propriété : A partir d'un certain rang :
Prenons n très très grand , Est-ce que ? Non bien évidemment.
Donc , clairement, ce n'est pas cette propriété qu'il faut démontrer.

Ce qu'il faut démontrer, c'est en fait : A partir d'un certain rang :

Mais apparemment, tu ne connais pas non plus cette notation
Déjà, ça se lit comment. Ca se lit Factorielle n. En cherchant ce mot Factorielle, tu devrais trouver plein d'explication sur cette opération.

En particulier, tu écris à un moment : n!= 1+2+6+24+120+...+n+(n+1) Je ne sais pas d'où ça sort, mais c'est faux.

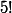ce n'est pas 1+2+6+24+120, c'est 120.

Pour déterminer ce , tu peux calculer et pour les premières valeurs de n (jusqu'à 6 ou 7, ça devrait suffire). Une fois ce déterminé, faudra voir pour la suite.

[LB2]

En fait tu n'as pas besoin de récurrence pour démontrer ça...
L'inégalité n! > n^2 est vraie à partir de n=4
On peut le démontrer directement en remarquant que (n-1)(n-2) > n à partir de n=4
et en minorant brutalement tous les autres facteurs (n-3), (n-4)..., 3, 2, 1 par 1.

[lyceen95]

Euh ... tu as relu ?

[Canehan]

Il y a plein de truc qui ne vont pas. Disons même que rien ne va.

Déjà, au moment de recopier l'énoncé, il y a une erreur.
Dans l'énoncé, tu dis qu'il faudrait montrer la propriété : A partir d'un certain rang $n_0$ : $n>n^2$
Prenons n très très grand , Est-ce que $n> n^2$ ? Non bien évidemment.
Donc , clairement, ce n'est pas cette propriété qu'il faut démontrer.

Ce qu'il faut démontrer, c'est en fait : A partir d'un certain rang $n_0$ : $n!>n^2$

Mais apparemment, tu ne connais pas non plus cette notation $n!$
Déjà, ça se lit comment. Ca se lit Factorielle n. En cherchant ce mot Factorielle, tu devrais trouver plein d'explication sur cette opération.

En particulier, tu écris à un moment : n!= 1+2+6+24+120+...+n+(n+1) Je ne sais pas d'où ça sort, mais c'est faux.

$5!$ ce n'est pas 1+2+6+24+120, c'est 120.

Pour déterminer ce $n_0$, tu peux calculer $n!$ et$ n^2$ pour les premières valeurs de n (jusqu'à 6 ou 7, ça devrait suffire). Une fois ce $n_0$ déterminé, faudra voir pour la suite.

En effet, navré pour l'erreur il faut démontrer n!>n^2

Je peux écrire n! + (n+1) = 1+2+6+24+120+...+n+(n+1) ou toujours pas ?
Je suis allé voir sur internet pour factorielle merci !
3! = 6 3^2= 9 et 6<9
4! = 24 4^2= 16 24>16
Donc la propriété st bien vraie à partir du rang 4. Dcnc $n_0$ = 4

[Canehan]

Donc la propriété est vraie au rang 4.
Je cherche à montrer qu'elle est vraie au rang n+1 après avoir admit qu'elle était vraie à un certains rang n+1.
Je cherche donc (n+1)!>(n+1)^2

[fatal_error]

soit la propriété P_n : n!> n^2
tu veux montrer qu'elle est vraie à partir d'un rang n_0.
est-ce que P_4 est vraie? 4! = 24, 4^2=16, 4!>4^2, oui
(tu as montré que P_3 est fausse) donc le plus petit n_0 tel que P_n est vraie est n_0 = 4.

Maintenant ton but c'est de montrer que P_n est vraie pour tout n>=4
tu as fait l'initialisation. (P_4 est vraie)
tu __ supposes __ P_n vraie pour un certain(sans s) n.

Tu veux montrer que SI P_n est vraie, alors P_{n+1} est vraie AUSSI
idem est-ce que (n+1)!>(n+1)^2 SI n!>n^2

[Canehan]

En effet je suis à la dernière étape avant la conclusion, seulement je ne comprend pas comment avancer dans l'étape de l'hérédité.
Il y a une équivalence pour (n+1)^2 ? ou pour n+&! ? Pouvant me permettre d'avancer ?
Merci

[GaBuZoMeu]

Pour passer de n! à (n+1)!, par quoi multiplie-t-on ?
Pour passer de n^2 à (n+1)^2, par quoi multiplie-t-on ?
Comment se comparent les deux facteurs ?

[Canehan]

Pour passer de n! à (n+1)!, par quoi multiplie-t-on ?
Pour passer de n^2 à (n+1)^2, par quoi multiplie-t-on ?
Comment se comparent les deux facteurs ?

Pour passer de n! à (n+1)! Je multiplie par (n+1) ce qui me donne n!*(n+1)=(n+1)!
exemple:
3! = 6
4! = 24
3!*4 = 6*4= 24

En revanche j'ai du mal à voir par quoi multiplier n^2 pour obtenir (n+1)^2

[GaBuZoMeu]

Ah bon ? Ne serait-ce pas par ?

[lyceen95]

Tu nous as redit : n! = 1+2+6+24+120 ... ... comme dans ton 1er message.

Mais non, c'est faux. Dans n!, on fait de multiplications, plein de multiplications, on ne fait pas d'addition.

5! , ce n'est pas 1+26+24+120 ou quelque chose comme ça, c'est 1*2*3*4*5=120.

[LB2]

Je maintiens qu'une preuve directe existe et est beaucoup plus efficace.
Si l'on veut absolument une récurrence, voici la preuve de l'hérédité :
Soit k tel que k! > k^2
(k+1)! = (k+1)*k! par définition
(k+1)*k! > (k+1)k^2 par hypothèse de récurrence au rang k
Or k^3+k^2 > k^2+2k+1 = (k+1)^2 car k>=4
donc (k+1)! > (k+1)^2 d'où l'hérédité