Primitive d'une fonction rationnelle

[ze zoune]

Bonjour à tous,

Après avoir longtemps cherché, je suis arrivé à un résultat dont je ne suis pas sûr.

Il s'agit de déterminer une primitive de la fonction

Mes calculs ont abouti à

Est-ce correct ?
Merci !

[Doraki]

Rien ne t'empêche de dériver F pour voir que ça colle pas du tout.

En particulier, ton F est dérivable en 0, et ton F' ne tend pas vers 2 en l'infini.

[ze zoune]

Comment faire alors pour calculer cette primitive ?

J'ai commencé par décomposer f en 3 parties distinctes:



J'ai ensuite cherché les primitives de chacune des parties et je suis tombé sur le résultat ci-dessus.

[girdav]

Bonjour,
la méthode conventionnelle consiste à écrire que puis à chercher et tels que .

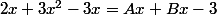
[ze zoune]

Effectivement il fallait y penser !

Merci beaucoup :) !

[girdav]

C'est un exercice de type classique : une fois que l'on connaît la méthode et que l'on comprend pourquoi elle fonctionne.
As-tu vu dans ton cours la décomposition en éléments simples d'une fraction rationnelle?

[ze zoune]

Oui maintenant qu'on en parle j'ai le souvenir d'avoir vu cela en exercice l'année dernière, mais je n'ai jamais noté la méthode quelque part !

[Ericovitchi]

La méthode c'est de poser

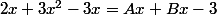
- tu multiplies les deux cotés par x et tu fais x=0 tu trouves A= ...
- tu multiplies les deux cotés par (x-3) et tu fais x=3 et tu trouves B= ...

[MacErmite]

Bonjour,

J'ai essayé de rechercher cette primitive et voilà ce que j'ai trouvé :

Décomposition de ensuite en décomposant en posant , ce qui conduit pour A=2 et B=2.

J'en conclue que ce qui conduit à , non ?

Cela fait un certain temps que je n'ai pas pratiqué ce genre de calculs, j'éspère ne pas avoir écris de bétises.

[ze zoune]

Bonjour !

C'est également ce que j'ai trouvé, maintenant je me bas avec d'autres exercices !
En gros cela signifie que je reviendrai régulièrement dans les prochains jours ^^ !