Primitive d'un quotient

par **abcdefghijkl** » 25 Mai 2013, 13:10

Bonjour,
pouvez vous m'aider à trouver une primitive du quotient tan u/cos u enfin je suis arrivé jusque là, au début fallait trouver une primitive de sqrt(1-x²)/x² en remplaçant x par cos u j'ai trouver ça merci de votre aide.

par **XENSECP** » 25 Mai 2013, 13:15

Hum remplace x par sin(u) et ce sera presque "fini" ;)

par **abcdefghijkl** » 25 Mai 2013, 13:19

au départ ?

par **XENSECP** » 25 Mai 2013, 13:21

euh oui au lieu de cos(u) quoi

par **abcdefghijkl** » 25 Mai 2013, 13:26

ca revient "presque" au meme a la fin je trouve cos u / sin² u

par **abcdefghijkl** » 25 Mai 2013, 13:27

abcdefghijkl a écrit:ca revient "presque" au meme a la fin je trouve cos u / sin² u

qui donne arctan u / sin u

par **XENSECP** » 25 Mai 2013, 13:33

Sachant que cos(u) est la dérivée de sin(u) ça te fait penser à rien le :

cos(u)/sin(u)^2 ?

par **abcdefghijkl** » 25 Mai 2013, 13:49

si cela donne donc -1/sin u donc une primitive de sqrt(1-x²)/x² est -1/sinarcsin x donc -1/x ? c'est ça?

par **XENSECP** » 25 Mai 2013, 14:46

Oula désolé j'étais pas réveillé.

avec

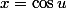
Or la dérivée de

est

Primitive d'un quotient

primitive d'un quotient

Qui est en ligne