Primitive Arg sh x ? [Résolu]

par **iZo** » 16 Oct 2007, 14:36

Salut,
Dans un exo sur les équations différentielles, pour chercher une solution particulière, je trouve

f " (x) = 1 / (1+x²)^1/2

Donc f ' (x) = Arg sh x = ln ( x + (1+x²)^1/2 )

Mais là problème : comment trouver une primitive de cette fonction?

Merci d'avance

par **Pythales** » 16 Oct 2007, 14:44

Par parties :

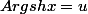
etc...

par **iZo** » 16 Oct 2007, 14:56

Je vois pas du tout ... pour faire par partie il faut un produit non?

par **Quidam** » 16 Oct 2007, 15:23

iZo a écrit:Je vois pas du tout ... pour faire par partie il faut un produit non?

Exact ! Mais Argsh(x)=argsh(x)*1 alors ça va aller !

par **iZo** » 16 Oct 2007, 19:30

Merci beaucoup j'ai réussi ;)

par **iZo** » 16 Oct 2007, 19:44

Arggg en fait j'ai une autre question:
Comment montrer que ch x > x ?
J'ai réussi sur pour x négatif, mais pas pour x positif ...

par **kazeriahm** » 16 Oct 2007, 20:37

salut

étudies la fonction x-> ch(x)-x

par **iZo** » 16 Oct 2007, 20:59

J'ai déjà essayé mais ça m'avance pas à grand chose...

par **Nightmare** » 16 Oct 2007, 21:08

Bonsoir :happy3:

Pour tout x positif,

et

On en déduit que

et ainsi

En intégrant sur [0;t] :

ie

:happy3:

par **iZo** » 16 Oct 2007, 21:55

Merci à vous tous ;)

Primitive Arg sh x ? [Résolu]

Primitive Arg sh x ? [Résolu]

Qui est en ligne