Manitwoo a écrit:Q1.1: Montrer que si
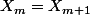
, alors
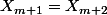
R1.1: J'ai donc écrit Soit

appartient K, On a
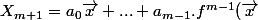+a_m.f^m(\vec{x})= X_m + a_m.f^m(\vec{x}))
Or
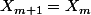
donc
=0.)
A partir de là, puis-je dire que
=0)
et donc l'endomorphisme est nilpotent d'ordre m ? Dans ce cas j'aurai
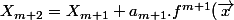)
avec
=0)
et donc
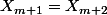
?
J'attends confirmation (ou infirmation ?) avant de publier la suite, et je vous remercie d'avance.
a0.x + a1.f(x) + ... + am.f^m(x) est un élément de X(m+1), ce n'est pas X(m+1).
De même, a0.x + ... + a(m-1).f^(m-1)(x) n'est pas X(m), et de toutes façon je ne sais pas ce que tu veux dire quand tu additionnes un sous-espace vectoriel avec un vecteur.
Donc non tu ne peux pas conclure que tous les endomorphismes sont nilpotents parceque c'est faux.
Par exemple, prend f(x) = x.
X(1) = Vect(x).
X(2) = Vect(x,f(x)) = Vect(x,x) = Vect(x) = X(1)
X(3) = Vect(x,f(x),f(f(x))) = Vect(x,x,x) = Vect(x) = X(2) ...
mais quand on prend un vecteur au hasard, f(f(x)) n'est pas forcément nul.
