Preuve par recurrence

[ludo56]

Bonjour,j'ai sous les yeux une preuve qui me rend perplexe:

Il s'agit de montrer qu'une suite est croissante et .
L'auteur procède comme suit:
il montre que par récurrence sur n.Il initialise donc et suppose vraie la propriété au rang n.En faisant cette hypothèse de récurrence,il montre que est croissante puis ce sert de cela pour montrer la propriété au rang n+1 cqfd.
Je n'arrive pas trop à voir si la croissance de la suite est démontrée de cette manière car on s'est quand même servi de l'hypothèse de récurrence pour conclure à cela.
Merci de votre aide

[girdav]

Bonjour,
il serait sans doute plus simple que tu nous donnes la suite en question. Elle doit sans doute être définie par une récurrence de la forme , avec une fonction suffisamment régulière.

[ludo56]

Oui,tu as raison il s'agit de la suite.
J'ai pu démontrer que cette suite qui est l'ensemble de définition de f et le but est maintenant de montrer que elle appartient à [a,c] ou c est l'unique racine de f (on suppose aussi f croissante convexe)
Mais ma question concerne plus la "construction de cette preuve"

[Doraki]

il montre aussi que xn est dans [a;c], dans la récurrence ?

[ludo56]

Oui.. Je n'ai pas été très clair désolé!
La récurrence est faite pour montrer que . Ma question est :il profite de l'hypothèse de récurrence pour montrer la croissance de ,ce qui me parait bizarre..

[Doraki]

Donc il montre par récurrence que pour tout n, (xn est dans [a;c] et xn+1 >= xn) ?

[ludo56]

Non,il montre bien que par récurrence que n, mais pour montrer l'hérédité,il utilise l'hypothèse de récurrence pour monter dans un premier temps que est croissante puis ce sert de ça pour conclure!

[Doraki]

Ben alors c'est comme si il montrait par récurrence que pour tout n, (xn est dans [a;c] et xn+1 >= xn), sauf que dans l'hypothèse de récurrence, il n'utilise pas (xn+1 >= xn).

[Ben314]

Vu l'énoncé, la logique de la preuve est de montrer que :
Si pour un certain n alors (*)
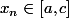
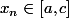
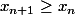
Ce qui, effectivement montre (par récurrence) que pour tout n mais aussi que la suite est croissante car, maintenant que l'on sait pour tout n, en utilisant l'implication (*), on en déduit que pour tout n.

P.S. :

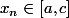
Non,il montre bien que par récurrence que n, mais pour montrer l'hérédité,il utilise l'hypothèse de récurrence pour monter dans un premier temps que est croissante puis ce sert de ça pour conclure!

Je pense que, là ou tu t'embrouille, c'est que, dans un premier temps, il de démontre absolument pas la croissance de la suite : il montre seulement que, si pour un certain n alors

[ludo56]

Merci beaucoup :we:
Donc finalement (si j'ai bien compris),lorsqu'on fait une preuve par récurrence,si l'hypothèse de récurrence implique une propriété au rang n,alors cette propriété sera vraie dès lors que la récurrence aboutit..C'est assez logique

[Ericovitchi]

tu peux aussi regarder là car on en a déjà parlé de ce problème.

[ludo56]

Disons que la question que j'ai posé concerne le "squelette" de la preuve. C'est en toute généralité que je demande ça!