Premier pas en analyse numérique

[Arckroz]

Bonjour,

Suite à ma non présence à un cour pour un empêchement, mon professeur a fait un exercice que je ne comprends pas et que je dois réviser rapidement;

On a f une fonction de Classe C^2, sur un intervalle fermé I. on suppose que f admet un unique zéro x* appartenant à I. On se donne comme paramètre b>0 et on définit la fonction g--> x - b f(x)

1) Montrer que g a un unique point fixe.

2) supposons que pour x appartenant a I, on ait m<f'(x)<M pour des constantes 0<m<M. Donner une condition suffisante pour b pour que g soit contractante.

3) on considère une suite définie par x(0) appartenant à I et x(n+1)= g(x(n)) pour n>0. Cette suite converge t'elle et comment choisir b pour que excepte suite converge avec la meilleure vitesse de convergence possible ?

4) Appliquer les questions précédentes à f(x)= x^2 - b. on supposera que b > 1 et on prendre I= intervalle (1,b).


Merci de votre aide car je ne comprends vraiment pas ce cours . Bonne journée a vous !

[Kolis]

Bonjour !
1. point fixe de si et seulement si si et seulement si .
Comme a un unique zéro, tu peux conclure...
2. est dérivable et .
Tu as donc l'encadrement (je respecte ton énoncé où les inégalités avec sont strictes mais j'ai de fort doutes sur le bon énoncé) et il est facile de trouver les conditions permettant de dire .
3. Il manque une donnée essentielle : la stabilité par de l'intervalle. Impossible de répondre, pas plus qu'aux questions suivantes, sans cette certitude.

[Ben314]

La stabilité, on peut tout a fait la démontrer, modulo de prendre b tel que pour tout vu que dans ce cas, le T.A.F. te dit que est compris entre 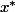et et vu que ces deux réels sont dans l'intervalle I le réel est lui aussi dans I.
Par contre, là où c'est embêtant, c'est que ça interdit de prendre un pour lequel g'(x)<0 pour certains x alors que pour que la vitesse de convergence soit la meilleure possible, il faudrait que |g'(x)| en valeur absolue reste le plus petit possible donc que g'(x) soit dans un intervalle du style [-k,k].

[Arckroz]

en effet erreur de ma part, dans l'énoncé pour la question 2n j'ai m <(ou égal) f'(x) <( ou égal) M pour des constantes 0 < m <(ou égal) à M.

[Arckroz]

donc pour la première question, alpha est un point fixe de g si g(alpha) = alpha donc d'un point de vue graphique c'est l'intersection de g et de la droite y=x

d'accord merci ^^

Du coup la numéro 2, et 3 je n'ai jamais vu cela, je ne vois pas comment y procéder

[Arckroz]

Pour tout x et y appartenant à I
J'ai g(x)-g(y) <k(x-y)

Donc pour x différent de y j'aurai

(x-y)(1- b (f(x)-f(y) / x-y ) < k(x-y) C'est des voleurs absolue pour k(x-y)

Je ne sais pas quoi faire pour la suite .

[Ben314]

Je comprend rien de ce que tu fait...
Tu en est à la question combien ?
D'où ça sort que tu as g(x)-g(y) <k(x-y) ?
C'est qui k là dedans ?

[Arckroz]

Désolé je suis à la question 2,3 que je bloque vu que j'en ai jamais fait

C'est la définition de contractante non ?

[Arckroz]

Je vous avoues que je suis perdu également !
J'étais pas présent à ce TD, et je veux revoir cet exercice avant le prochain TD. Mais Sans en avoir fait c'est compliqué

[Kolis]

Bonsoir !
En consultant le lien qui suit (un des derniers messages) j'ai des doutes sur ton histoire "absent en TD".
http://www.les-mathematiques.net/phorum/read.php?4,1542892.