Hello,
Je réécris juste l'énoncé pour me faciliter la tâche.
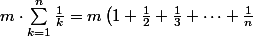 = m + \frac{m}{2} + \dots + \frac{m}{n})
Le PPCM est pair (pour k > 1) et, dans sa décomposition en facteurs premiers, la puissance de 2 est égale à la plus grande puissance de 2 parmi celles des nombres de 1 à n. Par exemples, si n = 10, la plus grande puissance de 2 est donnée par 8 uniquement et vaut 3; si n = 50, la plus grande puissance de 2 est donnée par 32 uniquement et vaut 5.
Or on divise le PPCM par chacun des nombres de 1 à n. Et on sait que la puissance de 2 du PPCM est donnée par un et un seul nombre. Donc, une seule de ces fractions sera un nombre impair, toutes les autres étant paires. Il en résulte que cette somme est un nombre impair.
J'espère que tu arriveras à déchiffrer mon charabias :mur: ,
Nerra