[statistique descriptive] Pourquoi le Quartile 2/4 est il différent de la médiane ?

[alone154]

Bonjour,
on m'a dit que sur les 3 quartiles d'une série statistique (14 , 2/4 , 3/4) que le 2eme était la médiane de la série statistique (meme sur wikipédia c'est écrit).
Or sous Maple quand je calcule la médiane, et le quartile 2, j'obtien des résultat différents (mais proche). Maple n'a pas tors,puisque quand j'applique la formule j'obtien le meme résultat . Quelqu'un saurais m'expliquer pourquoi le quartile 2 est différent de la médiane ?

[Quidam]

Il me semble que la définition de la médiane varie selon les auteurs. Cela pose souvent des problèmes !

L'un d'eux dira que c'est la valeur telle qu'il y a autant d'individu en dessous que d'individus au dessus ! Mais cette définition n'est pas claire, plus exactement, elle ne peut pas être toujours appliquée. Par exemple, s'il s'agit d'une note sur 20 et qu'on ne peut donner qu'un nombre entier de demi-points, si 284 individus ont une valeur inférieure ou égale à 11, 25 individu ont 11,5 et 273 individus ont plus que 11,5, alors il n'existe pas de valeur telle qu'il y ait autant d'individus au dessous qu'au dessus ! Si l'on choisit 11,5, on constate que 284 n'est pas égal à 273. Si l'on choisit un nombre plus grand on obtiendra au moins 284+25 individus en dessous de la valeur choisie, ce qui est plus que la moitié de la population, si l'on choisit un nombre plus petit on obtiendra au moins 273+25 individus au dessus de la valeur choisie, ce qui est également plus que la moitié de la population. Il n'y aurait pas de médiane ?

D'autres diront que c'est la plus petite valeur K telle que le nombre d'individu ayant une "valeur" inférieure ou égale à K, serait supérieur ou égal à la moitié de la population. Cette définition, elle, est parfaitement précise. Avec elle, la médiane de la population ci-dessus est 11,5 !

J'ai regardé plusieurs livres : en général, on sent un malaise en regardant la définition ! Lorsque l'on étudie les revenus des 60 000 000 français, le revenu médian a réellement un sens, mais ce n'est pas d'une grande importance de le définir au centime près, alors... Mais dans les problèmes posés au baccalauréat, s'il s'agit qu'un QCM, par exemple, une réponse presque juste est une réponse tout-à-fait fausse ! Il est déplorable qu'une définition précise ne fasse pas l'unanimité !

Je partage donc ta gêne !

Qu'en pensent les professeurs de mathématiques ?

[alone154]

Je ne manquerais pas la semaine prochaine de demander à mes professeurs de mathématiques, en espérant que du haut de leur thèse ils puissent expliquer
cette différence.
Quoi qu'il en soit je vous tiendrais au courant.

[paquito]

Effectivement, pour une série statistique discrète, la médiane est très mal définie.
Exemple: n=5 et X=(1,3,7;8,10); la médiane vaut 7 et le second quartile aussi, mais si on prends
n=4 et X=(1,3,8,10), une médiane peut être tout réel de l'intervalle ]3; 8[ ! La médiane n'est pas définie ! un logiciel affichera :
et , ce qui est un coup de cul, car si X=(2,3,8,10), mais .

Morale: à consommer avec modération car, effectivement, la médiane n'est pas bien définie et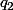 non plus d'ailleurs !!!

[Robot]

Paquito, tu te spécialises dans l'exhumation de vieux fils ?

[paquito]

J'essaie! en fait je cherche ma voie! il faudrait peut être que je trouve autre chose...