Pourquoi ne peux on pas composer les unicités et congruences

[Baptbe]

Bonjour,

J'ai eu cet exercice en DS de 1h ce matin (PCSI première année) et je n'ai absolument rien compris !
Possible de me donner des pistes ou de carrément m'expliquer ?
:mur:

https://www.dropbox.com/s/2c6n5wrcporv8bc/Maths%20DS%201

Merci.

[Kikoo <3 Bieber]

Salut,

On peut pas accéder au fichier

[Baptbe]

Salut,

On peut pas accéder au fichier

Oups, réessayez ici svp https://www.dropbox.com/s/2c6n5wrcporv8bc/Maths%20DS%201 ("télécharger" en haut à droite).

[Kikoo <3 Bieber]

Oups, réessayez ici svp https://www.dropbox.com/s/2c6n5wrcporv8bc/Maths%20DS%201 ("télécharger" en haut à droite).

Nan mais lol tu m'as renvoyé vers le même site :p

Le problème c'est que le fichier n'a aucune extension précise. De ce fait je ne peux pas le télécharger. En plus, qui me dit qu'il n'est pas infesté ?

Pourquoi ne pas recopier partiellement (au moins) l'énoncé ? L'ensemble peut être compréhensible si tu t'y prends bien.

[Baptbe]

[quote="Kikoo 0 ou (Ré(z)=0 et Im(z);)0)}

Montrer que (je traduis en Français) Pour tout u de C il existe un seul et unique z de P tel que z^2= u
Montrer que si z appartient à P il est en est de même.

[wserdx]

J'ai jeté un œil à ton document. Où bloques-tu?

[Baptbe]

Nan mais lol tu m'as renvoyé vers le même site :p

Le problème c'est que le fichier n'a aucune extension précise. De ce fait je ne peux pas le télécharger. En plus, qui me dit qu'il n'est pas infesté ?

Pourquoi ne pas recopier partiellement (au moins) l'énoncé ? L'ensemble peut être compréhensible si tu t'y prends bien.

C'est une photo (.png), ça ne craint rien !!

[Baptbe]

J'ai jeté un œil à ton document. Où bloques-tu?

En fait je comprends l'énoncé, mais je ne vois pas comment démontrer ça ! C'est entre guillemets logique, mais je ne sais pas comment démontrer ça formellement. De même pour l'exercice 2 ou il est évident qu'on à affaire au fait qu'une congruence est réfléxive, symétrique et transitive mais je ne vois pas par où commencer pour le démontrer.

Enfin, pour l'équation z^4=i je trouve une solution évidente grave à la formule de Moivres, mais je ne suis pas sûr de mes 3 autres !

[Kikoo <3 Bieber]

Je vais essayer mais c'est langage formelle !

On définit P la partie de ¢ par P : {z€¢/Ré(z)>0 ou (Ré(z)=0 et Im(z);)0)}

Montrer que (je traduis en Français) Pour tout u de C il existe un seul et unique z de P tel que z^2= u
Montrer que si z appartient à P il est en est de même.

Déjà essaie de visualiser le truc. P est la partie de des complexes dont la partie réelle est positive ou, si la partie réelle est nulle, ceux dont la partie imaginaire est positive. Tu peux donc hachurer (dans ta tête) le demi-plan droit privé de la demi-droite ]Oy) descendante du plan de Cauchy-Schwarz.

Prouve l'existence de z : Un nombre complexe de la forme a+ib avec a>0 peut-il être le carré d'un nombre u=x+iy de ?
Un imaginaire pur (avec b;)0) peut-il être carré d'un complexe ?

Prouve l'unicité de z : Montre la bijectivité de application de P dans

[Baptbe]

[quote="Kikoo 0 peut-il être le carré d'un nombre u=x+iy de ?
Un imaginaire pur (avec b;)0) peut-il être carré d'un complexe ?

Prouve l'unicité de z : Montre la bijectivité de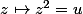 application de P dans [/quote]

Hum d'accord merci, et pour l'équation z^4=i une solution est bien e^i(;)/8) ? Pour trouver les autres il faut ensuite ajouter mod(2k;)/4) ? Soit ....i5;)/8 ....i9;)/8 et i13;)/5 ?

[wserdx]

En fait je comprends l'énoncé, mais je ne vois pas comment démontrer ça ! C'est entre guillemets logique, mais je ne sais pas comment démontrer ça formellement. De même pour l'exercice 2 ou il est évident qu'on à affaire au fait qu'une congruence est réfléxive, symétrique et transitive mais je ne vois pas par où commencer pour le démontrer.

Enfin, pour l'équation z^4=i je trouve une solution évidente grave à la formule de Moivres, mais je ne suis pas sûr de mes 3 autres !

Pour la première partie, il n'y a pas de difficulté si tu raisonnes en polaire.
La partie P, c'est les complexes d'argument tel que (plus le complexe 0)
Pour tout complexe, ses deux racines carrées sont décalées de , il n'y a donc qu'une seule qui "tombe" dans P.

Pour les congruences, tout consiste à trouver le qui convient.

[Baptbe]

Pour la première partie, il n'y a pas de difficulté si tu raisonnes en polaire.
La partie P, c'est les complexes d'argument tel que (plus le complexe 0)
Pour tout complexe, ses deux racines carrées sont décalées de , il n'y a donc qu'une seule qui "tombe" dans P.

Pour les congruences, tout consiste à trouver le qui convient.

Merci j'ai trouvé tout le raisonnement pour z^4=i avec 4 solutions, seulement 2 dans P puis 1 seule quand on élève au carrément (e^i;)/8).

Par contre pour les démonstrations 1, 2 et 3 je ne vois vraiment pas comment faire.