Pour une compréhention et pour me débloquer merci
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 22 Nov 2007, 22:36
par ptitmatteo » 22 Nov 2007, 22:36
oui car pour lexo davant il faut démontre le systeme que vs m'avais donner mais l'apliquer directement donc dure
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 22 Nov 2007, 22:36
par B_J » 22 Nov 2007, 22:36
en fait
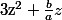
est le debut d'un carré
(
^2=x^2+2xy+y^2 \,\text{ avec}\, : \,x=z \,; \,2xy=\frac{b}{a}z)
)
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 22 Nov 2007, 22:38
par B_J » 22 Nov 2007, 22:38
ptitmatteo a écrit: B_J a écrit:^2-\frac{b^2}{4a}+\frac{4ac}{4a^2}=0)
c pourquoi??
c'est la suite du message #14
 par busard_des_roseaux » 22 Nov 2007, 22:41
par busard_des_roseaux » 22 Nov 2007, 22:41
je te propose la "méthode " suivante:
tu cherche une factorisation du polynôme sous la forme:
(x-a)(x-b)=(4x-6)(x-a)(x-b))
tu identifie les coefficients et tu calcule
S=a+b
P=ab
puis a et b sont solutions de l'équation:
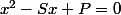
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 22 Nov 2007, 22:43
par ptitmatteo » 22 Nov 2007, 22:43
mais la on aura pas pareil car
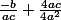
car sa fera -b²a
???
-
Quidam
- Membre Complexe
- Messages: 3401
- Enregistré le: 03 Fév 2006, 16:25
-
 par Quidam » 22 Nov 2007, 22:44
par Quidam » 22 Nov 2007, 22:44
ptitmatteo a écrit:mais pourle module sa va 'ai trouver
|z²|=racine{(-5)^2+12^2}=13
Non ! |z²| n'est pas égal à ça ; ça, c'est |z| !
Donc |z²| = (-5)^2+12^2
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 22 Nov 2007, 22:45
par B_J » 22 Nov 2007, 22:45
ptitmatteo a écrit:mais la on aura pas pareil car
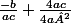
car sa fera -b²a
???
d'où vient ca ?
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 22 Nov 2007, 22:47
par B_J » 22 Nov 2007, 22:47
Quidam , c'est z^2=-5+12i
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 22 Nov 2007, 22:47
par ptitmatteo » 22 Nov 2007, 22:47
B_J a écrit:^2-\frac{b^2}{4a}+\frac{4ac}{4a^2}=0)
donc si on mas sur le meme dénominateur
sa fera -ab² é pas -b² se kon doit trouver
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 22 Nov 2007, 22:48
par ptitmatteo » 22 Nov 2007, 22:48
(x-a)(x-b)=(4x-6)(x-a)(x-b))
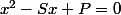
comment fai tu pour trouversa?
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 22 Nov 2007, 22:50
par B_J » 22 Nov 2007, 22:50
desolé , c'est une erreur de ma part ; j'ai corrigé
on a plutot
^2-\frac{b^2}{4a^2}+\frac{4ac}{4a^2}=0)
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 22 Nov 2007, 22:57
par ptitmatteo » 22 Nov 2007, 22:57
pour la B
il dise de démontre
si j'ai bien compris on fais fait le delta de az²+bz+c=0
?
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 22 Nov 2007, 22:57
par B_J » 22 Nov 2007, 22:57
as-tu compris la a) ?
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 22 Nov 2007, 22:58
par ptitmatteo » 22 Nov 2007, 22:58
oui enfait moi je suis parti pas s que j'avais é apré j'étais bloquer
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 22 Nov 2007, 23:01
par B_J » 22 Nov 2007, 23:01
pour la b)
on a
^2=\frac{\Delta}{4a^2}=\frac{\delta^2}{4a^2}=(\frac{\delta}{2a})^2)
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 22 Nov 2007, 23:02
par ptitmatteo » 22 Nov 2007, 23:02
car delta=b²-4ac
donc z=
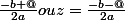
mais la je démontre pas??
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 22 Nov 2007, 23:04
par B_J » 22 Nov 2007, 23:04
-
ptitmatteo
- Membre Relatif
- Messages: 454
- Enregistré le: 03 Déc 2006, 15:17
-
 par ptitmatteo » 22 Nov 2007, 23:04
par ptitmatteo » 22 Nov 2007, 23:04
B_J a écrit:pour la b)
on a
^2=\frac{\Delta}{4a^2}=\frac{\delta^2}{4a^2}=(\frac{\delta}{2a})^2)
pas compris la??
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 22 Nov 2007, 23:07
par B_J » 22 Nov 2007, 23:07
on a montré que l'equation de depart est equivalente a :
^2-\frac{\Delta}{4a^2}=0)
or le premier membre de cette egalité est une difference de deux carrés
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 22 Nov 2007, 23:09
par B_J » 22 Nov 2007, 23:09
n'oublie pas que
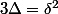
par hypothese
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
