Bonjour!Besoin s'un coup de main Merci
exercice:
Determiner les transformée de laplce des fonctions causales suivantes:
1)f(t)=(2-te^(-2t))U(t)
=>f(t)=(2-te^(-2t))U(t) =2U(t)-te^(-2t)U(t)
F(p)=2/p - 1/p² = 2/p -1/(p+2)²
2)g(t)=sin(t-pi/3)U(t-pi/3)
=>soit f(t)=sin tU(t)
alors F(p)= 1/p²+1
et g(t)=f(t-pi/3)
donc g(t)=F(p)e^(pi/3 p) = e^(-pi/3 p) / p²+1
3)h(t)=cos(2t) U(t-pi/2)
=> =cos(2t-pi/2+pi/2)U(t-pi/2)
=cos(2t-pi/2)U(t-pi/2)
Je n'arrive pas a terminer!
4)k(t)=cos(pit)e^(-2t)U(t)
K(t)= p-2 / (p-2)²+pi
Exercice n°2:
Determiner la transformée du signal,apres l'avoir écrit a l'aide de l'échelon unité:
http://www.hiboox.com/image.php?img=a21324fb.jpg
Je ne sais pas comment faire
Exercice n°3
Déterminer l'expression,en fon,ction de U(t),du signal ci-dessous et calculer sa transformée:
http://www.hiboox.com/image.php?img=a21324fb.jpg
=>f(t)=(U(t)-U(t-1))+t(U(t-1)-U(t-2))+(U(t-2)-U(t-3))+((-1/5t)+1)(U(t-3)-U(t-5))
F(p=(1/p - 1/pe^(-p))+ je n'arrive pas a continuer!
Exercie n°4:
F(p)=p²+3p-1 / p²(p-2)
G(p)=p+2 / (p²+2p+2)(p+1)
H(p)=(1/p + 1/p²)e^(-p)
Je ne sais pas se qu'il faut faire!!Merci d'avance
DM pour demain sur laplace
14 messages
- Page 1 sur 1
par floriane15963 » 19 Fév 2007, 21:10
Oula ,escusez moi c'est pour quel exercice ca car ca ma plutot l'aire d'etre assez complexe!!
par floriane15963 » 19 Fév 2007, 21:23
je n'est pas d'exponentiel par contre dans le 1-3 c juste
"cos(2t) U(t-pi/2)"
"cos(2t) U(t-pi/2)"
par mathelot » 19 Fév 2007, 21:31
Dans l'exercice 2, je ne comprend pas la représentation graphique de la fonction
pour
. La fonction est nulle , c'est cela ?
La fonction de l'exercice (2), je vé l'intégrer à la main:
dt=\int_{0}^{2} e^{-pt}f(t)dt+\int_{2}^{4} e^{-pt}f(t)dt)
la courbe de f est symétrique par rapport à la droite d'équation x=2.
f(2-h)=f(2+h).
dt=\int_{0}^{2} e^{-2p+pu}f(2-u)du+\int_{0}^{2} e^{-2p-pu}f(2+u)du)
du+\int_{0}^{2} e^{-2p-pu}f(2+u)du=2e^{-2p}\int_{0}^{2} \quad ch(pu) f(2-u) du)
 f(2-u) du=2e^{-2p}\int_{0}^{2} \quad ch(p(2-t)) f(t) dt=2e^{-2p} \left( \int_{0}^{1} \quad ch(p(2-t)) dt +\int_{1}^{2} \quad ch(p(2-t)) (-2t+4) dt \right))
je te laisse terminer ce calcul.
pour
La fonction de l'exercice (2), je vé l'intégrer à la main:
la courbe de f est symétrique par rapport à la droite d'équation x=2.
f(2-h)=f(2+h).
je te laisse terminer ce calcul.
par mathelot » 19 Fév 2007, 22:16
Il y a peut être plus simple si l'on arrive à exprimer la fonction à intégrer de l'exercice (2) en fonction de U. Mais ça, je ne sais pas faire.
Quelques pistes pour l'exo (4):
d'après la formule:
d \tau \right)= \frac{1}{p}L(f))
.
}=\frac{1}{p}+\frac{5}{p^2}+\frac{9}{p^{2}(p-2)})
les originaux de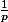
, de 
et })
sont connus.
Il restera à primitiver l'original de
http://fr.wikipedia.org/wiki/Transform%C3%A9e_de_Laplace#Quelques_transform.C3.A9es_usuelles
pour trouver l'original de
(p+1)})
,
on décompose en éléments simples:
(p+1)}=\frac{ap+b}{{(p+1)}^2+1}+\frac{c}{p+1})
on prend l'original de chaque terme.
La prochaine fois, ne poste pas tes dm la veille.
Bonne nuit. :dodo:
Quelques pistes pour l'exo (4):
d'après la formule:
les originaux de
Il restera à primitiver l'original de
http://fr.wikipedia.org/wiki/Transform%C3%A9e_de_Laplace#Quelques_transform.C3.A9es_usuelles
pour trouver l'original de
on décompose en éléments simples:
on prend l'original de chaque terme.
La prochaine fois, ne poste pas tes dm la veille.
Bonne nuit. :dodo:
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :