Re-post
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
simplet
- Membre Relatif
- Messages: 374
- Enregistré le: 29 Oct 2005, 12:28
-
 par simplet » 29 Déc 2005, 13:52
par simplet » 29 Déc 2005, 13:52
Je reposte un probleme auquel on a encore jamais repondu completement, et ca m'interesserai de savoir le resoudre...
g une application de G vers G
g(x)= x*x*x
montrer que si g est un morphisme surjectif alors (G,*) est abbelien
:mur:
(merci)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Déc 2005, 14:23
par Nightmare » 29 Déc 2005, 14:23
Bonjour
Soit y dans G, puisque f est surjective, il existe z dans G tel que y=z^3
Soit x dans G, comme f est un morphisme, on a :
^{3}=x^{3}z^{3}x^{-3})
, d'où :
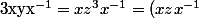^{3}=x^{3}z^{3}x^{-3}=x^{3}yx^{-3})
donc
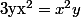
^{2}y=(xy)^{3}=x^{3}y^{3}=x(x^{2}y^{2})y)
donc
^{2}=x^{2}y^{2}=(x^{2}y)y=(yx^{2})y=(yx)(xy))
d'où
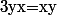
Q.E.D
:happy3:
-
Fract83
- Membre Relatif
- Messages: 110
- Enregistré le: 25 Nov 2005, 13:35
-
 par Fract83 » 29 Déc 2005, 14:50
par Fract83 » 29 Déc 2005, 14:50
Hello,
Nightmare, t'es en 1ere, et tu maitrises deja les groupes...!!
Ca me fait peur... C'est comme un cauchemard :-)
Plus serieusement, t'es conscient que c'est au programme du superieur (en France tout du moins) ce que tu viens de faire ? C'est impressionnant...
Ciao.
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 29 Déc 2005, 15:00
par yos » 29 Déc 2005, 15:00
Bonjour,
je suis désolé de voir que certaines réponses passent à la trappe. GALT a répondu complètement à la question, dans le précédent Post. On a parfois l'impression que des questions sont posées et que les réponses ne sont pas lues.
Voilà.
Bon on va pas en faire un plat.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 29 Déc 2005, 15:05
par Nightmare » 29 Déc 2005, 15:05
C'est la base de la sup ça frac83 ce n'est pas bien difficile, je parviens déjà plus difficilement à résoudre certains probléme que les profs de sup donnent en DS
:happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
