Positionnement aléatoire dans une sphère
21 messages
- Page 1 sur 2 - 1, 2
Positionnement aléatoire dans une sphère
Positionnement aléatoire dans une sphère. J'aimerais calculer une probabilité dans une situation qui exige un niveau en math excédant largement mes pauvres compétences.
1
Dans une sphère de 4 mètres de diamètre, on place un certain nombre de points au hasard.
Combien de points sont nécessaires pour avoir 1 chance sur 2 de placer deux points à moins d'un millimètre l'un de l'autre ?
2 - (Indépendamment que la question 1)
J'ai 1000 minutes pour placer un certain nombre de points. Chaque point est placé n'importe quand, durant ces 1000 minutes. Il n'est visible que pendant 60 secondes.
Combien de points sont nécessaires pour avoir 1 chance 2 d'apercevoir simultanément deux points ?
(Simultanément signifie ici "chevauchement". Par exemple : un point est visible de 13:07 à 14:06. Un autre est visible de 13:50 à 14:49 )
3
Combien faut il de points pour remplir simultanément les conditions 1 et 2 ?
(Les événements étant indépendants, je suppose qu'on multiplie les deux probabilités.)
Pour 1, le chevauchement de petites sphères dans une grande, je ne vois même pas l'outil permettant d'exprimer la limitation de distance.
Pour 2, Le paradoxe des anniversaires est une version de ce problème avec une définition beaucoup plus simple de la concomitance (pas de "chevauchement" partiel). Donc la résolution est facile.
1
Dans une sphère de 4 mètres de diamètre, on place un certain nombre de points au hasard.
Combien de points sont nécessaires pour avoir 1 chance sur 2 de placer deux points à moins d'un millimètre l'un de l'autre ?
2 - (Indépendamment que la question 1)
J'ai 1000 minutes pour placer un certain nombre de points. Chaque point est placé n'importe quand, durant ces 1000 minutes. Il n'est visible que pendant 60 secondes.
Combien de points sont nécessaires pour avoir 1 chance 2 d'apercevoir simultanément deux points ?
(Simultanément signifie ici "chevauchement". Par exemple : un point est visible de 13:07 à 14:06. Un autre est visible de 13:50 à 14:49 )
3
Combien faut il de points pour remplir simultanément les conditions 1 et 2 ?
(Les événements étant indépendants, je suppose qu'on multiplie les deux probabilités.)
Pour 1, le chevauchement de petites sphères dans une grande, je ne vois même pas l'outil permettant d'exprimer la limitation de distance.
Pour 2, Le paradoxe des anniversaires est une version de ce problème avec une définition beaucoup plus simple de la concomitance (pas de "chevauchement" partiel). Donc la résolution est facile.
On ne saurait aller chercher trop loin le plaisir de rentrer chez soi.
Re: Positionnement aléatoire dans une sphère
des pistes par un pas pro des probas :
pour la 1
-> en négligeant les effet de bord, un raisonnement sur le volume d'une sphère de rayon 1mm et une loi binomiale (sans doute à transformer vu que p va être très petit) me semble possible.
pour la 2 :
-> un raisonnement en moyenne ne nous ramène-t-il pas une loi uniforme ?
Pseuda est pas par là ?
pour la 1
-> en négligeant les effet de bord, un raisonnement sur le volume d'une sphère de rayon 1mm et une loi binomiale (sans doute à transformer vu que p va être très petit) me semble possible.
pour la 2 :
-> un raisonnement en moyenne ne nous ramène-t-il pas une loi uniforme ?
Pseuda est pas par là ?
Modifié en dernier par pascal16 le 24 Oct 2018, 19:39, modifié 2 fois.
Re: Positionnement aléatoire dans une sphère
Bonjour,
La question posée n'appelle pas de réponse : voir (facile à trouver sur Internet) le paradoxe de Bertrand,
et on part cependant d'une situation bien plus simple...
La piste évoquée par Pascal16 est tout à fait plausible (si j'ai bien compris, tirer au hasard parmi un nombre fini de sphères définies à l'avance), encore faut il préciser qu'on fait ce tirage là, et non partir de l'énoncé de soleildetenebre.
Bon courage à qui veut aller plus loin
Rdvn
La question posée n'appelle pas de réponse : voir (facile à trouver sur Internet) le paradoxe de Bertrand,
et on part cependant d'une situation bien plus simple...
La piste évoquée par Pascal16 est tout à fait plausible (si j'ai bien compris, tirer au hasard parmi un nombre fini de sphères définies à l'avance), encore faut il préciser qu'on fait ce tirage là, et non partir de l'énoncé de soleildetenebre.
Bon courage à qui veut aller plus loin
Rdvn
Re: Positionnement aléatoire dans une sphère
Salut,
Concernant la question 1., je sais répondre dans un cas beaucoup plus simple qui est le suivant :
On fixe un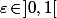 . On tire au hasard (avec répartition uniforme)
. On tire au hasard (avec répartition uniforme)  réels de l'intervalle
réels de l'intervalle  .
.
Quel est la proba. que deux d'entre eux soient à une distance
que deux d'entre eux soient à une distance 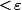 ?
?
\varepsilon\Big)^{\!\!n}\text{ si }n\!\leq\!1\!+\!\frac{1}{\varepsilon}\ \text{ et }\ p\!=\!1\ \text{ sinon})
Après, on peut tenter de faire comme si ça marchait plus ou moins pareil sur la sphère avec égal au rapport entre la surface d'un disque de rayon 1mm et la surface de la sphère.
égal au rapport entre la surface d'un disque de rayon 1mm et la surface de la sphère.
Je pense que ça risque de donner un "ordre de grandeur" du résultat, mais je suis pas sûr du tout que ce soit vraiment très pertinent comme approximation.
EDIT : Et sauf erreur, ce "cas plus simple" répond exactement à la question 2. (avec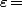 60 sec / 1000 min)
60 sec / 1000 min)
Concernant la question 1., je sais répondre dans un cas beaucoup plus simple qui est le suivant :
On fixe un
Quel est la proba.
Après, on peut tenter de faire comme si ça marchait plus ou moins pareil sur la sphère avec
Je pense que ça risque de donner un "ordre de grandeur" du résultat, mais je suis pas sûr du tout que ce soit vraiment très pertinent comme approximation.
EDIT : Et sauf erreur, ce "cas plus simple" répond exactement à la question 2. (avec
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Positionnement aléatoire dans une sphère
J'avais interprété le "dans la sphère" comme un problème volumique. "Sur la sphère" serait surfacique à coup sur.
Re: Positionnement aléatoire dans une sphère
En tout cas, y'a un truc de sûr, c'est que ce soit "sur la sphère" ou "dans la sphère", ben ça change rien concernant le fait que... je sais pas faire...
Dans , je sais le faire car on peut ordonner les éléments
, je sais le faire car on peut ordonner les éléments 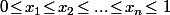 et qu'une fois ordonnés, la condition "deux d'entre eux sont à une distance <
et qu'une fois ordonnés, la condition "deux d'entre eux sont à une distance < " devient extrêmement simple à étudier.
" devient extrêmement simple à étudier.
Mais comme il n'y a rien d'équivalent ni "sur la sphère", ni "dans la sphère" . . .
Dans
Mais comme il n'y a rien d'équivalent ni "sur la sphère", ni "dans la sphère" . . .
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Positionnement aléatoire dans une sphère
Rdvn a écrit:La question posée n'appelle pas de réponse : voir (facile à trouver sur Internet) le paradoxe de Bertrand,
Le paradoxe de Bertrand se décompose en 3 cas de figure tous solubles. Une telle réponse me suffirait.
pascal16 a écrit:J'avais interprété le "dans la sphère" comme un problème volumique.
C'est ça. "Dans la sphère" signifie ici dans le volume délimité par la sphère.
Ben314 a écrit:
ce "cas plus simple" répond exactement à la question 2
Tu trouves combien ?
Je ne comprends pas ton calcul mais c'est bien la situation : dans un segment temporel de 1000 minutes, la probabilité de choisir 2 points à moins de 60 secondes l'un de l'autre, sachant qu'on en choisit n.
Perso, j'évaluais la probabilité de non concomitance des deux premiers points à (1000 - 2) / 1000. 1000 - 2 étant l'espace restant au deuxième. Pour le troisième, (1000 - 4) / 1000 etc.
Jusqu'au énième point qui a une probabilité de (1000 - 2(n-1))/1000 de ne rencontrer personne.
Du coup, on obtient facilement la probabilité qu'il y ait une apparition simultanée d'au moins deux des points. Il n'y a plus qu'à résoudre p = 1/2. Mais ça me semble d'une simplicité suspecte.

PS : je n'ai pas su intégrer au message mon résultat en LaTeX. Le forum ne lit pas le LaTeX ?
$$p_n=1 - \frac{(1000-2)\times (1000-4)\times \cdots \times (1000-2(n-1))}{1000^\left(n-1 \right)}$
Modifié en dernier par soleildetenebres le 25 Oct 2018, 12:00, modifié 1 fois.
On ne saurait aller chercher trop loin le plaisir de rentrer chez soi.
Re: Positionnement aléatoire dans une sphère
Bonjour
A l'attention de soleildestenebres
Ce n'est pas ça du tout : Bertrand montre qu'en trois tirages différents, il obtient trois réponses différentes, afin de montrer qu'il n'y a aucun sens à la phrase "quelle est la probabilité de ..." , si c'est détaché des précisions nécessaires sur le tirage aléatoire. En réalité on pourrait trouver encore d'autres tirages, mais ces trois là suffisent pour décrire une situation paradoxale, pour illustration :
http://therese.eveilleau.pagesperso-ora ... rtrand.htm
Pour votre problème, il faudrait savoir ce que vous choisissez...
En outre, l'aspect tridimensionnel rendra la résolution très compliquée, sauf réduction volontaire de la complexité du tirage : la première piste évoquée par Pascal16 étant très réaliste...
Bonne suite
Rdvn
A l'attention de soleildestenebres
Ce n'est pas ça du tout : Bertrand montre qu'en trois tirages différents, il obtient trois réponses différentes, afin de montrer qu'il n'y a aucun sens à la phrase "quelle est la probabilité de ..." , si c'est détaché des précisions nécessaires sur le tirage aléatoire. En réalité on pourrait trouver encore d'autres tirages, mais ces trois là suffisent pour décrire une situation paradoxale, pour illustration :
http://therese.eveilleau.pagesperso-ora ... rtrand.htm
Pour votre problème, il faudrait savoir ce que vous choisissez...
En outre, l'aspect tridimensionnel rendra la résolution très compliquée, sauf réduction volontaire de la complexité du tirage : la première piste évoquée par Pascal16 étant très réaliste...
Bonne suite
Rdvn
Re: Positionnement aléatoire dans une sphère
Rdvn a écrit:Pour votre problème, il faudrait savoir ce que vous choisissez
J'aimerais avoir plusieurs solutions contradictoires dues à des conditions expérimentales mal définies, comme dans l'énoncé initial du paradoxe de Bertrand. Mais là j'ai zéro solution, zéro point de départ.
On ne saurait aller chercher trop loin le plaisir de rentrer chez soi.
Re: Positionnement aléatoire dans une sphère
soleildetenebres a écrit:Tu trouves combien ?
Je ne comprends pas ton calcul mais c'est bien la situation : dans un segment temporel de 1000 minutes, la probabilité de choisir 2 points à moins de 60 secondes l'un de l'autre, sachant qu'on en choisit n.
Perso, j'évaluais la probabilité de non concomitance des deux premiers points à (1000 - 2) / 1000. 1000 - 2 étant l'espace restant au deuxième. Pour le troisième, (1000 - 4) / 1000 etc.
Jusqu'au énième point qui a une probabilité de (1000 - 2(n-1))/1000 de ne rencontrer personne.
Du coup, on obtient facilement la probabilité qu'il y ait une apparition simultanée d'au moins deux des points. Il n'y a plus qu'à résoudre p = 1/2. Mais ça me semble d'une simplicité suspecte.
Concernant la partie bleue :
- Ce que je trouve, c'est que, si
- Si tu veut le détail de comment je trouve ce résultat (et comment j'en déduit l'approximation ci dessus) je peut te le mettre (mais j'ai pas le temps tout de suite).
Sinon, concernant ton raisonnement, ça donne sans doute un "ordre de grandeur" du résultat, mais ça risque d'être pas mal faux vu que tu fait comme si chaque nouveau point ajouté enlevait forcément un segment de 2 de long à l'ensemble des "valeurs acceptables", alors que ce n'est pas le cas : si le nouveau point ajouté est à moins de 2 unités d'un point déjà présent, la "zone qu'il enlève" fait moins de 2 de large vu qu'elle chevauche la zone enlevé par l'autre point. Pour les premiers points, ça change pas grand chose vu que la proba. que le nouveau point soit à moins de 2 d'un autre est faible, mais quand le nombre de points va augmenter, ça va être différent.
Sans parler du fait qu'avec ta façon de procéder, il faudra ensuite faire un produit de pas mal de "proba élémentaires" pour avoir le résultat et qu'un petite erreur sur chacune de ces proba. élémentaires risque de compromettre grandement la fiabilité du résultat.
Modifié en dernier par Ben314 le 25 Oct 2018, 20:23, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Positionnement aléatoire dans une sphère
raisonnement loufoque... mais pas trop
volume total/volume d'une bille de 1mm de rayon : (2000)^3=M
en ne tenant strictement pas compte du fait qu'on peut déjà avoir des shpères qui se chevauchent déjà à l'étape n
p la proba de de rencontre entre un point déjà placé et sa sphère de 1mm de rayon
je place 1 point : po=0
le place un point p1=1/M
je place un second point : p2= 2/M car mon calcul est faux par excès
....
soit à résoudre n(n+1)/2 =(2000)^3 /2
n = 89444, valeur par excès
le calcul de Ben donne 74 466
Maintenant, je vais tenter le calcul en binomiale transformée en normale, poisson ou exp, le calcul sera par défaut car l’appartenance d'un point à une sphère de 1mm autour d'un autre point ne dit pas que les sphères ont même centre.
Si découpe la grande sphère en éléments finis (genre un pas de 1/(10n) mm), puis on passe à la limite, le problème d'égalité de position saute, ça semble plus fin comme résultat
volume total/volume d'une bille de 1mm de rayon : (2000)^3=M
en ne tenant strictement pas compte du fait qu'on peut déjà avoir des shpères qui se chevauchent déjà à l'étape n
p la proba de de rencontre entre un point déjà placé et sa sphère de 1mm de rayon
je place 1 point : po=0
le place un point p1=1/M
je place un second point : p2= 2/M car mon calcul est faux par excès
....
soit à résoudre n(n+1)/2 =(2000)^3 /2
n = 89444, valeur par excès
le calcul de Ben donne 74 466
Maintenant, je vais tenter le calcul en binomiale transformée en normale, poisson ou exp, le calcul sera par défaut car l’appartenance d'un point à une sphère de 1mm autour d'un autre point ne dit pas que les sphères ont même centre.
Si découpe la grande sphère en éléments finis (genre un pas de 1/(10n) mm), puis on passe à la limite, le problème d'égalité de position saute, ça semble plus fin comme résultat
Re: Positionnement aléatoire dans une sphère
Ben314 a écrit: tu fait comme si chaque nouveau point ajouté enlevait forcément un segment de 2 de long à l'ensemble des "valeurs acceptables", alors que ce n'est pas le cas
Tu as raison, je pars de la proba d'une non concomitance avec un étalement optimal des points. En laissant des espaces "perdus" entre les points (par exemple 45 secondes), l'espace restant pour les points suivants serait réduit d'autant, Et la probabilité de non concomitance serait réduite aussi.
Du coup, "ma" probabilité de non concomitance est maximale.
Donc mon résultat final, événement contraire, est la probabilité minimale d'avoir au moins deux points visibles en même temps. Et donnerait la valeur minimale de n (p croissante). Je veux la première valeur de n qui fait passer p au dessus de 1/2. Donc celle là.
Ben314 a écrit:siest suffisamment petit, pour avoir
, il faut prendre
Tu trouves
pascal16 a écrit:raisonnement loufoque... mais pas trop
volume total/volume d'une bille de 1mm de rayon : (2000)^3=M
Moi, j'aime bien. L'espace total V est la somme de M volumes élémentaires v. Je pourrais refaire mon raisonnement. Dans une disposition optimale ne créant pas d'espace non utilisable entre les points :
- la probabilité de placer un deuxième point sans chevauchement est (V - v)/V
- la probabilité du troisième : (V - 2v)/V
- la probabilité du énième : (V - v ( n - 1 ))/V
De là, on tire la valeur maximale de la probabilité de l'absence d'un quelconque chevauchement entre deux des n points. Puis la valeur minimale de la probabilité d'un chevauchement d'au moins deux points. Et le n correspondant.

pascal16 a écrit:soit à résoudre n(n+1)/2 =(2000)^3 /2
Je n'ai pas compris pourquoi (2000)^3 /2
On ne saurait aller chercher trop loin le plaisir de rentrer chez soi.
Re: Positionnement aléatoire dans une sphère
somme des probas =1/2 <=> (n(n+1)/2)*(1/(2000)^3) = 1/2
r grande sphere= 2m = 2000 mm
rapport de volume petite sphère de 1mm vs grand sphère de 2000mm = 1/(2000)^3
r grande sphere= 2m = 2000 mm
rapport de volume petite sphère de 1mm vs grand sphère de 2000mm = 1/(2000)^3
Re: Positionnement aléatoire dans une sphère
Ta somme va de p1 à p(n-1), il me semble. Donc n(n-1)/2.
Quoiqu'il en soit, j'aime bien, même si tu restreins la situation de départ. Ce que tu calcules, si j'ai bien compris, c'est la probabilité que la deuxième chevauche la première + la probabilité que la troisième chevauche sachant que les deux premières ne se chevauchent pas entre elles + la probabilité que la quatrième chevauche sachant que les trois premières ne se chevauchent pas entre elles etc. Autrement dit, la probabilité d'un seul chevauchement entre 2 des n sphères.
Quoiqu'il en soit, j'aime bien, même si tu restreins la situation de départ. Ce que tu calcules, si j'ai bien compris, c'est la probabilité que la deuxième chevauche la première + la probabilité que la troisième chevauche sachant que les deux premières ne se chevauchent pas entre elles + la probabilité que la quatrième chevauche sachant que les trois premières ne se chevauchent pas entre elles etc. Autrement dit, la probabilité d'un seul chevauchement entre 2 des n sphères.
Modifié en dernier par soleildetenebres le 27 Oct 2018, 03:06, modifié 2 fois.
On ne saurait aller chercher trop loin le plaisir de rentrer chez soi.
Re: Positionnement aléatoire dans une sphère
oui, c'est seulement par excès.
on peut améliorer avec du p(1)-p(2)+p(3)-p(4)....
mais je me dis que je rate une solution bien plus simple qui a déjà du être écrite.
de plus je suis tombé sur des considérations de chevauchements incomplet des sphères.
du coup le passage par la limite me paraissait mieux indiqué
on peut améliorer avec du p(1)-p(2)+p(3)-p(4)....
mais je me dis que je rate une solution bien plus simple qui a déjà du être écrite.
de plus je suis tombé sur des considérations de chevauchements incomplet des sphères.
du coup le passage par la limite me paraissait mieux indiqué
Re: Positionnement aléatoire dans une sphère
pascal16 a écrit:je me dis que je rate une solution bien plus simple qui a déjà du être écrite
Pareil. C'est tout de même un problème assez simple. Il doit exister une approche plus adaptée.
On ne saurait aller chercher trop loin le plaisir de rentrer chez soi.
Re: Positionnement aléatoire dans une sphère
Je suis pas sûr du tout que le problème soit "simple" en dimension autre que 1 vu que rien que le calcul du "chevauchement" de deux boules de même rayon en dimension autre que 1, ça donne une formule pas simple. Et j'imagine pas vraiment une méthode exacte pour évaluer la proba que tu demande qui n'utiliserait pas une telle formule (c'est peut-être là que je me goure).
Regarde rien qu'en dimension 2, si tu as deux disques de rayon 1 situés à une distance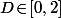 l'un de l'autre, quelle est la surface recouverte pas les deux disques.
l'un de l'autre, quelle est la surface recouverte pas les deux disques.
A mon avis, un truc qui pourrait éventuellement simplifier le problème, c'est de changer de métrique et de prendre la distance de Manhattan (=celle issue de la "norme infinie") où les "chevauchement" sont bien plus facile à calculer.
Regarde rien qu'en dimension 2, si tu as deux disques de rayon 1 situés à une distance
A mon avis, un truc qui pourrait éventuellement simplifier le problème, c'est de changer de métrique et de prendre la distance de Manhattan (=celle issue de la "norme infinie") où les "chevauchement" sont bien plus facile à calculer.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Positionnement aléatoire dans une sphère
Ben314 a écrit:Si tu veut le détail de comment je trouve ce résultat (et comment j'en déduit l'approximation ci dessus) je peut te le mettre (mais j'ai pas le temps tout de suite).
Un lien me suffira si la résolution existe en ligne.
On ne saurait aller chercher trop loin le plaisir de rentrer chez soi.
Re: Positionnement aléatoire dans une sphère
C'est sûrement déjà connu, mais comme je sais pas où chercher un lien, je te fait la preuve (pas longue) :
On fixe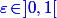 et
et 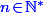 . On tire aléatoirement
. On tire aléatoirement  réels
réels 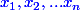 de l'intervalle
de l'intervalle 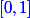 en suivant une loi uniforme et avec indépendance. Quelle est la proba.
en suivant une loi uniforme et avec indépendance. Quelle est la proba. 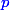 qu'au moins deux d'entre eux soient à une distance
qu'au moins deux d'entre eux soient à une distance  ?
?
On s’intéresse plutôt à la proba.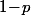 de l’événement contraire qui est la mesure de l'ensemble
de l’événement contraire qui est la mesure de l'ensemble \!\in\![0,1]^n\text{ t.q. }\forall i\!\not=\! j\!\in\!\{1..n\},\ |x_i\!-\!x_j|\!\geq\!\varepsilon\}) divisée par la mesure de l'ensemble "total"
divisée par la mesure de l'ensemble "total" 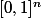 qui vaut 1.
qui vaut 1.
Sauf que le fait d'être (ou pas) dans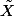 est indépendant de l'ordre dans lequel sont les
est indépendant de l'ordre dans lequel sont les  (1) donc
(1) donc 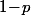 , c'est la mesure de l'ensemble
, c'est la mesure de l'ensemble \text{ t.q. }0\!\leq\!x_1\!\leq\!x_2\!\leq...\leq\!x_n\!\leq\!1\text{ et }\forall i\!\in\!\{1..n\!-\!1\},\ x_{i+1}\!-\!x_i\!\geq\!\varepsilon\}) divisé par la mesure de
divisé par la mesure de \text{ t.q. }0\!\leq\!x_1\!\leq\!x_2\!\leq...\leq\!x_n\!\leq\!1\}) .
.
Ensuite, si on considère la fonction qui à) associe
associe \!=\!\big(x_1,x_2\!-\!\varepsilon,x_3\!-\!2\varepsilon,...,x_n\!-\!(n\!-\!1)\varepsilon\big)) c'est une translation (donc une isométrie bijective) et l'ensemble
c'est une translation (donc une isométrie bijective) et l'ensemble  a la même mesure que l'ensemble
a la même mesure que l'ensemble \!=\!\{(y_1,...y_n)\text{ t.q. }0\!\leq\!y_1\!\leq\!y_2\!\leq...\leq\!y_n\!\leq\!1\!-\!(n\!-\!1)\varepsilon\}) qui, s'il est non vide (2), est un homothétique de
qui, s'il est non vide (2), est un homothétique de  par un rapport
par un rapport \varepsilon\!>\!0) et qui a donc une mesure égale à celle de
et qui a donc une mesure égale à celle de  multipliée par
multipliée par 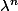 ce qui signifie que
ce qui signifie que 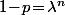 .
.
(1) Et si on est pas convaincu, on peut le démontrer "proprement" en utilisant l'ensemble et les application
et les application \mapsto (x_{\sigma(1)},...x_{\sigma(n)})) où
où  est une des
est une des  permutation de
permutation de 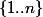 (qui sont clairement des isométries)
(qui sont clairement des isométries)
(2) C'est à dire si\varepsilon\!\geq\!0) soit encore
soit encore 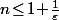
On fixe
On s’intéresse plutôt à la proba.
Sauf que le fait d'être (ou pas) dans
Ensuite, si on considère la fonction qui à
(1) Et si on est pas convaincu, on peut le démontrer "proprement" en utilisant l'ensemble
(2) C'est à dire si
Modifié en dernier par Ben314 le 01 Nov 2018, 14:14, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Positionnement aléatoire dans une sphère
Ensuite, concernant la résolution de 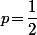 , c'est à dire
, c'est à dire \varepsilon\big)^{\!n}\!=\!\dfrac{1}{2}) , ça équivaut à
, ça équivaut à \varepsilon\big)\!=\!-\!\ln(2)) donc à
donc à \varepsilon\!\approx\!-\!\ln(2)) en supposant
en supposant \varepsilon) relativement petit donc à
relativement petit donc à ) en supposant
en supposant  relativement grand donc à
relativement grand donc à }{\varepsilon}}) .
.
- Si est assez petit, un tel
est assez petit, un tel  va être assez grand et ça justifie la deuxième approximation
va être assez grand et ça justifie la deuxième approximation \!\approx\!n^2) .
.
- Avec un tel assez grand, on a
assez grand, on a \varepsilon\!\approx\!n\varepsilon\!=\!\sqrt{\ln(2)\varepsilon}) qui est relativement petit si
qui est relativement petit si  est petit et ça justifie la première approximation.
est petit et ça justifie la première approximation.
- Si
- Avec un tel
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
21 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
