Polytope
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 06 Oct 2014, 19:29
par Cliffe » 06 Oct 2014, 19:29
Bonjour,
Comment savoir simplement si l'ensemble des solutions de l'équation
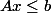
forme un polytope ? Avec

,

et
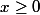
.
Merci.
-
mathelot
 par mathelot » 07 Oct 2014, 06:30
par mathelot » 07 Oct 2014, 06:30
..................
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 07 Oct 2014, 09:19
par Cliffe » 07 Oct 2014, 09:19
On connaît

et

bien sûr.
-
mathelot
 par mathelot » 07 Oct 2014, 09:39
par mathelot » 07 Oct 2014, 09:39
bonjour,
Soit S l'ensemble des solutions. C'est un fermé.
De la compacité de S, j'en ai déduit
 \in [1;m|])

je ne sais si c'est bon et si ça sert.
exemple, pour le carré unité de

, et la norme
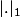




le souci, c'est que le numéro de ligne en question dépend de la solution (x,y) ??
dans le 1er quadrant, c'est la ligne 2 qui est positive.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 07 Oct 2014, 16:57
par zygomatique » 07 Oct 2014, 16:57
Cliffe a écrit:Bonjour,
Comment savoir simplement si l'ensemble des solutions de l'équation
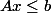
forme un polytope ? Avec

,

et
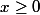
.
Merci.
salut
que signifie x >= 0 ?
chaque ligne du système Ax = b est équivalente à l'équation = b_i qui est l'équation d'un hyperplan et donc la relation <= b_i définit un demi-espace
et tu cherches l'intersection de ces n demi-espaces ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
mathelot
 par mathelot » 07 Oct 2014, 17:12
par mathelot » 07 Oct 2014, 17:12
les notations sont évidentes mais as tu la solution ?
d'après ce que j'en ai compris, il ne faut pas que S ait une composante connexe non bornée.
S doit être compact. Le souci, dans le petit exemple que j'ai fourni, bien que
la boule unité , pour la norme 1, soit bornée, il y a tout de même des coefficients de la matrice négatifs.
-
mathelot
 par mathelot » 07 Oct 2014, 17:26
par mathelot » 07 Oct 2014, 17:26
il faut lire ça
surprenant

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Oct 2014, 17:33
par Ben314 » 07 Oct 2014, 17:33
Salut,
Je viens de farfouiller à droite/à gauche sur le Net pour trouver la définition de "polytope" (moi et les définition, ça fait 2...)
Vu que je suis pas sûr à 100%, le problème c'est bien de savoir si l'ensemble

est une partie borné ou pas ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 07 Oct 2014, 17:34
par Cliffe » 07 Oct 2014, 17:34
Non je n'ai pas la solution.

avec

le vecteur nul.
polytope = polyèdre convexe.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 07 Oct 2014, 17:38
par zygomatique » 07 Oct 2014, 17:38
Cliffe a écrit:Non je n'ai pas la solution.

avec

le vecteur nul.
polytope = polyèdre convexe.
il me semble plutôt que c'est une convention pour dire que chaque coordonnée de x est positive ....
effectivement le problème est donc de montrer que c'est borné ...
et donc puisque on prend x >0 il suffit de tester avec x = 0
si A0 < b (quoique je ne comprenne pas cette notation ...) alors 0 appartient au "bon côté" de chaque demi-espace et donc à leur intersection et l'ensemble des solutions est borné ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
mathelot
 par mathelot » 07 Oct 2014, 17:39
par mathelot » 07 Oct 2014, 17:39
Ben314 a écrit:Salut,
Je viens de farfouiller à droite/à gauche sur le Net pour trouver la définition de "polytope" (moi et les définition, ça fait 2...)
Vu que je suis pas sûr à 100%, le problème c'est bien de savoir si l'ensemble

est une partie borné ou pas ?
oui, c'est nécessairement un fermé comme image réciproque d'un fermé par une application continue.
un théorème dit que c'est borné
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 07 Oct 2014, 17:40
par Cliffe » 07 Oct 2014, 17:40
zygomatique a écrit:il me semble plutôt que c'est une convention pour dire que chaque coordonnée de x est positive
bah oui. x_i >= 0 pour tout i si tu préfères.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Oct 2014, 17:44
par Ben314 » 07 Oct 2014, 17:44
C'est quoi qui est surprenant ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Cliffe
- Membre Rationnel
- Messages: 967
- Enregistré le: 12 Juin 2012, 13:25
-
 par Cliffe » 07 Oct 2014, 17:45
par Cliffe » 07 Oct 2014, 17:45
Ben314 a écrit:
est une partie borné ou pas ?
Oui c'est ça. Je pense que c'est assez simple.
-
mathelot
 par mathelot » 07 Oct 2014, 17:45
par mathelot » 07 Oct 2014, 17:45
zygomatique a écrit:si A0 < b (quoique je ne comprenne pas cette notation ...) alors 0 appartient au "bon côté" de chaque demi-espace et donc à leur intersection et l'ensemble des solutions est borné ....


contient O mais n'est pas borné

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Oct 2014, 17:46
par Ben314 » 07 Oct 2014, 17:46
mathelot a écrit:un théorème dit que c'est borné
Si A est la matrice nulle, je pense pas que ce soit borné...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 07 Oct 2014, 17:47
par zygomatique » 07 Oct 2014, 17:47
mathelot a écrit:

contient O mais n'est pas borné
sauf qu'on a aussi la condition x >= 0 ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
mathelot
 par mathelot » 07 Oct 2014, 17:48
par mathelot » 07 Oct 2014, 17:48
ce qui est surprenant est le fait que S soit borné (sous certaines conditions) est un théorème
signé Minkowski,Steiniz,Weyl.
Quelles sont les conditions et est-ce trivial ?
-
mathelot
 par mathelot » 07 Oct 2014, 17:51
par mathelot » 07 Oct 2014, 17:51
zygomatique a écrit:sauf qu'on a aussi la condition x >= 0 ....
ah,oui....
d'après la remarque de zygomatique,

d'autre part S est convexe
 \leq tb)
Ay \leq (1-t)b)
y) \leq b)
S est convexe , étoilé.

n'est pas borné
<br />\left(<br />\begin{array}<br />x \\<br />y<br />\end{array}<br />\right)<br />\leq <br /><br />\left(<br />\begin{array}<br />1 \\<br /> 1 <br />\end{array}<br />\right))

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Oct 2014, 17:54
par Ben314 » 07 Oct 2014, 17:54
Perso, j'aurais tendance à penser qu'en utilisant des arguments de compacité de la sphère unité, on devrait pouvoir montrer que

est non borné ssi il contient une "demi droite", c'est à dire un ensemble de la forme

Aprés quelques gribouillages, je conjecturerais bien que

est borné ssi il existe un vecteur
ligne 
tel que

et

Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
forme un polytope ? Avec
,
et
.
avec
le vecteur nul.
