MacManus a écrit:En supposant que P et Q ont des racines distinctes (P1 P2 Q1 et Q2 en utilisant tes notations), on voit que dans les factorisations de P et Q en polynômes de degré 1, aucun de ces polynômes ne sont multiples l'un de l'autre également. Donc il n'y a aucun polynôme de degré 1 qui divise à la fois P et Q. Donc P et Q sont premiers entre eux.
D'autres part si l'on observe dans la factorisation une racine commune pour P et Q, alors P et Q ne sont pas premiers entre eux!
[...]
1)C'est ça: pour être plus explicite tu peut dire que si P et Q ont une racine commune r alors (X-r) divise P et Q donc P et Q ne sont pas premiers.
Reciproquement si P et Q ne sont pas premiers entre eu alors:
-Soit il y a un polynome de degrès 2 qui les divise les deux donc tu peut dire ici qu'on est en contradiction avec l'enoncé ou alors ce qu'a dis léon (je pense que la précison inutile de l'énoncé sert à alléger la réponse).
-Soit il y a un polynome de degrès 1: k.(X-r) qui divise P et Q et dans ce cas r est forcement racine de P et de Q.
Même démo si l'un des polynome est de dégrès 3.
2)P et Q on ici une racine commune r et leur autre racine respectivement P_1 et Q_1 est differente si on considère qu'il sont non multiple l'un de l'autre (la encore cette hypothèse n'est pas indispensable effectivement).
Tu écrit donc
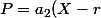 (X-P_1))
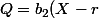 (X-Q_1))
A partir de la tu devrait pouvoir resoudre la première partie de la question.
Pour la deuxième partie,
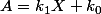
(avec k_1 non nul) donc
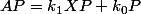
ect... (au final tu doit trouver une décomposition de 0 sous forme
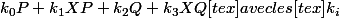
non tous nuls).
3)Par contraposé, si XP, P, Q, et XQ sont linéairement dépendants alors il éxiste
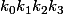
non tous nuls tel que
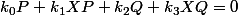
donc il existe A et B polynomes de degrès 0 ou 1 tels que AP=BQ donc A et B ne sont pas premiers entre eux (a monter en faisant la réciproque de la question 2).
