Polynômes

par **Easyblue** » 24 Oct 2007, 10:10

Bonjour!
J'ai la formule suivante:
(1-X)P'(X)-nP(X)=aX^(n-1)
Je dois trouver les coefficients de P et la valeur de a (P est un polynôme de degré srticement plus petit que n)
J'ai essayé de dériver n-1 fois puis n-2 fois...mais cette méthode me paraît un peu longuette et je ne suis pas sûre d'arriver au résultat.
N'auriez-vous pas une méthode plus simple?

par **tize** » 24 Oct 2007, 13:14

Bonjour,
tu peux poser

et ensuite lance toi...

devient :...

par **Easyblue** » 24 Oct 2007, 13:47

tize a écrit:Bonjour,
tu peux poser et ensuite lance toi... devient :...

Oui c'est bon j'ai fait ça mais je trouve (-2n+1)a(n+1)=a et je crois qu'il faut trouver a(n-1)=a mais je sais pas où est mon erreur??????????

par **nuage** » 24 Oct 2007, 15:29

Salut,
Si il y a une erreur elle est peut-être dans l'énoncé.
Avec celui que tu donnes je trouve aussi

,
Et il est rare que deux personnes fassent exactement la même erreur dans un calcul.

par **tize** » 24 Oct 2007, 15:35

devient :

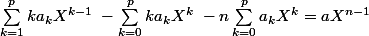
avec un changement d'indice :

ou encore :

et comme

je trouve la même chose que nuage :

par **Easyblue** » 24 Oct 2007, 17:49

Non c'est moi qui me sui trompée. J'ai fait avec "une autre métode" et pour moi -(n-1)-n=1 :briques:
C'est bonj'ai compris.
Merci à vous

par **GARGARENSIS** » 03 Nov 2007, 17:57

salut à tous! eske kelkun serai en mesure de me donner la méthode pour factoriser un polynome à coefiscients complexes?

merci d'avance!

Polynômes

Polynômes

Urgent!!

Qui est en ligne