Bonjour,
j'ai un exercice type sur les polynomes que j'aimerais comprendre sa méthode de résolution:
Trouver tous les polynomes de IK[X] de d°n tq P-P'=X^n/n!
Merci.
Polynomes
4 messages
- Page 1 sur 1
par Nightmare » 04 Fév 2007, 13:13
Bonjour
On remarque d'abord que si P vérifie l'égalité, deg(P)=n
On note
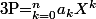
Essaye alors de travailler sur les coefficients.
Par exemple tu sais que
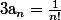
Ensuite
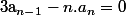
donc...
etc.
On remarque d'abord que si P vérifie l'égalité, deg(P)=n
On note
Essaye alors de travailler sur les coefficients.
Par exemple tu sais que
Ensuite
etc.
par tize » 04 Fév 2007, 13:14
Bonjour,
il suffit d'écrire=\sum\limits_{k=0}^{n}a_kX^k)
on a-P'(X) = a_nX^n + \sum\limits_{k=0}^{n-1}\(a_k-(k+1)a_{k+1}\)X^k=\frac{X^n}{n!})
De là on trouve facilement tous les coefficients
il suffit d'écrire
on a
De là on trouve facilement tous les coefficients
par fahr451 » 04 Fév 2007, 13:30
f : Rn[X] -> Rn[X] P ->P-P' est un isomorphisme de R espaces vectoriels
ce qui garantit a priori existence et unicité de l'antécédent de X^n/n!
ce qui garantit a priori existence et unicité de l'antécédent de X^n/n!
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :