Soient A,B €C[X], n€N* fixé, w1,...,wn les racines nième de l’unité
1- montrer que A^n-B^n =\prod_{k=1}^{n}{A-wkB}
2- On a S(a,b) l’ensemble des polynômes non constants vérifiant P(x^2)=P(X+A)P(X+b) d’inconnue .
En déduire que si P€C[X] et si P^n€S(a,b) alors P€S(a,b)
Polynômes
7 messages
- Page 1 sur 1
Re: Polynômes
Bonjour,
pour le 1 on doit pouvoir résonner avec les racines (comptés avec leur multiplicité).
pour le 1 on doit pouvoir résonner avec les racines (comptés avec leur multiplicité).
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
Re: Polynômes
Bonjour,
pour le premier, si est racine de
est racine de  alors
alors -B^n(z)=\prod_{k=1}^n{(A(z)-\omega_k B(z))}) de façon évidente. Si
de façon évidente. Si \neq 0) alors tu peux utiliser la factorisation
alors tu peux utiliser la factorisation 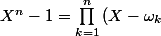})
pour le premier, si
Re: Polynômes
mathelot a écrit:d'ailleurs, si tu ne résonnes pas, on va te sonner les cloches..
Zut, j'ai été doublé

Re: Polynômes
Tuvasbien a écrit:Bonjour,
pour le premier, siest racine de
alors
de façon évidente. Si
alors tu peux utiliser la factorisation
D’accord merci bcp ! Je dois passer à côté d’un truc c’est quoi l’évidence ?
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
