Polynomes

[c1m2l3e]

Bonjour, je suis bloquée sur cet exercice, pouvez vous m'aider?
f: R+ --> R: x>cos(sqrt(x))
a) Si x appartient à R*+, calculer f''(x), en déduire la limite de f'' en 0.
J'ai trouvé f'' = (-cos(sqrt(x))+(sin(sqrt(x))/sqrt(x)))/4x mais je n'arrive pas à trouver la limite en 0

b) Montrer que f est deux fois dérivable en 0 et préciser f''(0)
Peut-etre avec un développement limité mais je n'aboutis pas

c)En déduire que f est de classe C² sur R+

d) Montrer que f admet un développement limité à tout ordre en 0.

e) Donner des polynomes P1 et Q1 tels que : xf''(x) = P1(x)f(x) + Q1(x)f'(x)
J'ai trouvé P1 = -1 et Q1 = -2

f) En dérivant la relation précédente, donner des polynomes P2 et Q2 tels que x²f'''(x) = P2(x)f(x) + Q2(x)f'(x)
J'ai trouvé P2 = 3/8 et Q2 = -(x-3)/4

g) Montrer l'existence de suites (Pn) et (Qn) où n>=1 telles que x^nf(n+1)(x) = Pn(x)f(x) + Qn(x)f'(x)
Peut-être par récurrence mais je n'arrive pas à faire l'hérédité


Merci par avance

[aviateur]

Bonjour
Peux tu utiliser les balises Latex c'est tout de même mieux à lire!!
Pour f''(x) cela me semble correct.
Pour la limite moi je ferai un petit DL (au voisinage de 0):


Tu remplaces cela dans f''(x) est tu vas trouver la limite.
Je te laisse faire et donnes le résultat s-t-p

[c1m2l3e]

Tout d'abord, merci d'avoir répondu.
Je trouve 1/12
Pourtant pour la question d'après, j'avais fait le DL de f à l'ordre 2 et j'avais 1/24 comme coefficient devant x², ce qui correspond à f''(0) non?

[aviateur]

Bonjour, oui c'est bon et ton DL est bon aussi.
En effet le DL, la partie principale en général correspond au développement de Taylor, i.e


Donc si tu trouves 1/24 alors 1/24=1/2*f'(0) , tout est cohérent.

[c1m2l3e]

Pour trouver la valeur de la dérivée en 0, il faut donc diviser le coefficient par l'ordre? Pour f''' ce sera le coefficient devant x^3 divisé par 3?

[aviateur]

Non par 6 de façon générale c'est n!

[c1m2l3e]

Ah oui pardon, merci j'ai compris.
Je pense avoir réussi la b) et la c), pouvez vous m'aider pour la d)?

[aviateur]

Tu me demandes de l'aide pour d) alors que je n'ai pas encore vu b) et c) .
En 2 mots qu'est ce que tu as trouve pour b et c ?

[aviateur]

L'exercice n'est pas si simple j'espère que b et c sont corrects.

[c1m2l3e]

Excusez moi,
pour la b) j'ai fait le développement limité à l'ordre 2, vu qu'elle en a un, f est deux fois dérivable en 0 et f''(0) = 1/12
pour la c), vu que f'' tend vers 1/12 = f''(0), elle est continue en 0 et vu que f est Cinf sur R*+, f est C² sur R+

Pouvez vous me dire ce que vous en pensez?

[aviateur]

Je pense que b n'est pas correct.
Pour le c) on peut voir ça après mais je crois que c'est bon.
Attention c'est un exercice très technique (très formateur mais il ne faut pas sauter des étapes)
Revenons à b) Il faut savoir qu'une fonction de classe au voisinage de 0 (encore que ici c'est + compliqué car on travaille sur 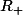) admet un DL a tout ordre mais la réciproque est fausse.

Donc pour montrer que f est dérivable 2 fois en zéro tu ne peux pas utiliser le DL mais revenir à la définition:

Résumons avant tout, c'est clair que f est sur
"Le seul problème est dc en zéro" est il faut faire les choses proprement:
As tu démontré que f dérivable en zéro? Non je ne pense pas;
Il faut commencer par cela en erd (= en revenant à la définition).
(f(x)-f(0))/x a-t-il une limite et tend vers quoi qd x tend vers 0( je sais dl mais...)

[c1m2l3e]

J'avais utilisé le fait qu'on avait un développement limité à l'odre un mais je suppose que ça ne marche pas du coup...
Ca fait (cos(sqrt(x))-1 )/ x
(Désolé je n'arrive pas à écrire la formule autrement)

[c1m2l3e]

Et la limite ce serait -1/2 si on utilise un développement limité?

[aviateur]

Pour écrire en latex tu mets \ devant sqrt et puis tu utilises éditeur complet et tu sélectionnes la partie math en cliquant sur tex. C'est simple comme bonjour.

Effectivement d'où (f(x)-1)/x=... et tend vers .... donc f est dérivable en zéro
et f'(0)=.....
Et tu recommences de façon analogue avec f''(0),... i.e
(f(x)-f'(0))/x=.....

[c1m2l3e]

(f(x)-1)/x = -1/2 + o(1) qui tend vers -1/2 donc f est dérivable en 0 et f'(0) = -1/2

Pour f'', j'ai:

Il faut faire un développement limité aussi?

[aviateur]

Oui un petit DL pour le sinus . attention -(-1/2)=+1/2.

[c1m2l3e]

Ca fait -1/12+o(1) donc f' est dérivable en 0 et f''(0)=-1/12
C'est ça?

[c1m2l3e]

Euh +1/12 plutôt

[aviateur]

oui c'est ça.
le c) maintenant. ?

[c1m2l3e]

vu que f'' tend vers 1/12 = f''(0), elle est continue en 0 et vu que f est Cinf sur R*+, f est C² sur R+