Polynômes : relation coefficients/nombre de racines

[nonam]

Bonjour, voilà un exercice qui me pose problème :

Soit
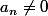
On suppose que et qu'il existe au moins deux entiers k tels que
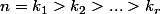
On note les indices k vérifiant et pour ,
on pose si [TEX]a_{k_i}a_{k_{i+1}} 0
de P et de P'.
Celà serait vraiment sympa si quelqu'un pouvait me débloquer.

[ThSQ]

C'est la règle des signes de Descartes (enfin une des règles), cf google (avec Descartes' Rule of Signs aussi)

Pas évident de résoudre ça sans indication. C'est un exo d'oral ?

[nonam]

Merci ! J'ai pu trouver une démo qui suivait la même démarche que celle que je voulais suivre : récurrence sur le degré, et relation avec P' pour montrer l'hérédité. Finalement j'étais pas très loin d'y arriver...
Non c'est pas un exo d'oral, je l'ai sorti d'un livre. Ce serait effectivement chaud de tomber sur un truc pareil à l'oral.

[ThSQ]

Merci ! J'ai pu trouver une démo qui suivait la même démarche

Cool :++:

[mathelot]

une démonstration directe ne me paraît pas évidente du tout.

as tu essayé d'utiliser le théorème de Rolle ?

[nonam]

je l'utilise un peu dans la démonstration par récurrence, mais je ne vois pas bien comment l'utiliser pour éviter la récurrence...