Bonjour,
j'essaye de faire l'épreuve de maths de l'X 2005 en PC dont le pdf se trouve à cette adresse, et je bloque à la question 4.a., où il est question de trouver une espèce de relation de récurrence entre polynômes orthogonaux, construits avec une méthode type Gram-Schmidt.
Elle ne m'a pas l'air si dure que ça, mais je n'arrive à rien.
Merci de bien vouloir m'aider!
Gary
(Je précise que je passe cette année en spé PC).
Polynômes orthogonaux (X 2005 PC)
9 messages
- Page 1 sur 1
Ce n'est pas laborieux si on s'y prend bien.
On cherche et
et  tels que
tels que
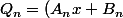P_{n-1} + C_nP_{n-2}) satisfasse au conditions 1,2 et 3. On laisse de coté 1 et 3 pour commencer.
satisfasse au conditions 1,2 et 3. On laisse de coté 1 et 3 pour commencer.
On remarque d'abord que pour m<n-2 on a=0) par linéarité en utilisant que
par linéarité en utilisant que  = (P_{n-1}|xP_m)=0.)
En suite on a
 = 0)
ce qui revient à
 + B_n \alpha_{n-1}^2=0)
et
 = 0) ce qui revient à
ce qui revient à
 + C_n \alpha_{n-2}^2=0.)
C'est un sytème de deux équations à trois inconnues. On pose en paramètre et on a
en paramètre et on a
}{\alpha_{n-1}^2})
et
}{\alpha_{n-2}^2}) .
.
Bref on a donc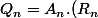) où
où 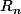 est fixe. Il suffit alors de choisir
est fixe. Il suffit alors de choisir  pour que 3 soit satisfait.
pour que 3 soit satisfait.
Ici on ne démontre que l'existence, et on ne fait donc pas les calculs.
On cherche
On remarque d'abord que pour m<n-2 on a
En suite on a
ce qui revient à
et
C'est un sytème de deux équations à trois inconnues. On pose
et
Bref on a donc
Ici on ne démontre que l'existence, et on ne fait donc pas les calculs.
Merci Yipee, je n'aurais pas dû bloquer là-dessus... :mur:
Pour Tize:
puisque) forme une base de
forme une base de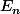 , tu peux déduire de la condition 2 que pour tout n
, tu peux déduire de la condition 2 que pour tout n 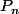 appartient à l'orthogonal de
appartient à l'orthogonal de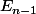 . Or
. Or  est de degré n et
est de degré n et  de degré au plus n-3 donc ces deux polynômes sont orthogonaux. De même pour
de degré au plus n-3 donc ces deux polynômes sont orthogonaux. De même pour 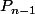 qui est de degré n-1 et
qui est de degré n-1 et  de degré au plus n-2. J'espère avoir été clair. :lol3:
de degré au plus n-2. J'espère avoir été clair. :lol3:
Gary
Pour Tize:
puisque
Gary
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
