[L1] Polynômes et nombres de Bernoulli.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 21 Mar 2012, 18:39
Bonjour!
Merci de m'aider dans la progression de ce problème.
On rappelle :
!})
On définit :
 = 1 \\<br />\forall n \geq 1, B_n(X) \, = \, \sum_{k=0}^n \binom nk b_k X^{n-k}<br />\end{array}<br />\right.)
1) Vérifier que :
 \, = \, B_n(1) \, = \, b_n)
2) Démontrer que :
 \, = \, n B_{n-1}(X))
3) En déduire que :
.dt \, = \, 0)
4) Etablir par récurrence que :
 - B_n(X) \, = \, n X^{n-1})
5) En déduire que :
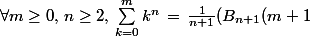 - B_{n+1}(0)))
6)
 \, = \, (-1)^n B_n(1-X))
6.a) Démontrer que la suite
)
est confondue avec la suite
)
6.b) En déduire que :
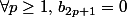
7) 7.a) Montrer que :
}(t)B_n(t).dt \, = \, b_n \times (f^{(n-1)}(1) - f^{(n-1)}(0)) - n \times (\bigint_{0}^{1} f^{(n-1)}(t)B_{n-1}(t).dt))
7.b) En déduire que :
!} \, \bigint_{0}^{1} f^{(2k+1)}(t)B_{2k+1}(t).dt \, = \, - \frac{b_{2k}}{(2k)!} \, (f^{(2k-1)}(1) - f^{(2k-1)}(0)) \, + \, \frac{1}{(2k-1)!} \, \bigint_{0}^{1} f^{(2k-1)}(t)B_{2k-1}(t).dt)
7.c) Montrer alors la première formule d'Euler-Mac Laurin :
dx \, = \, \frac{f(0)+f(1)}{2} \, - \, \sum_{k=1}^p b_{2k} \frac{f^{(2k-1)}(1) - f^{(2k-1)}(0)}{(2k)!} \, - \, \frac{1}{(2p+1)!} \bigint_{0}^{1} f^{(2p+1)}(t)B_{2p+1}(t).dt)
D'avance merci.
PS : je poste ci-dessous ce que j'ai fait, et là où je bloque.
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 21 Mar 2012, 18:46
1) Pour tout
, on a :
 \, = \, \bigsum_{k=0}^{n} \binom nk b_k 0^{n-k} \, = \, \bigsum_{k=0}^{n-1} 0 + \binom nn b_n \, = \, b_n)
 \, = \, \bigsum_{k=0}^{n} \binom nk b_k \, = \, \bigsum_{k=0}^{n-1} \binom nk b_k + \binom nn b_n \, = \, b_n)
D'où :  = B_n(1) = b_n)
Est-ce juste?
2) J'ai commencé... sans résultat concluant :
 \, = \, \bigsum_{k=0}^{n} \binom nk b_k (n-k) X^{n-k-1} = \bigsum_{k=0}^{n} \frac{n!}{k!(n-k-1)!} b_k X^{n-k-1})
Et :
 \, = \, \bigsum_{k=0}^{n-1} \frac{(n-1)!}{k!(n-k-1)!} b_k X^{n-k-1})
D'où :
 \, = \, \bigsum_{k=0}^{n-1} \frac{n!}{k!(n-k-1)!} b_k X^{n-k-1})
Est-ce juste? Est-ce un bon départ?
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
par ev85 » 21 Mar 2012, 18:54
Deluxor a écrit:1) Pour tout
, on a :
D'où : Est-ce juste?
2) J'ai commencé... sans résultat concluant :
Et :
D'où :
Est-ce juste? Est-ce un bon départ?
Oui pour la 1) Tu craignais quoi ?
Pour la 2) tu as songé à la formule de Taylor ?
amicalement,
e.v.
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 21 Mar 2012, 18:55
ev85 a écrit:Pour la 2) tu as songé à la formule de Taylor ?
amicalement,
e.v.
Bonsoir
ev85,
Est-ce que ce que j'ai noté pour la 2) est juste, ou sinon, qu'est-ce qui est faux?
Merci.
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
par ev85 » 22 Mar 2012, 09:27
Deluxor a écrit:Bonsoir ev85,
Est-ce que ce que j'ai noté pour la 2) est juste, ou sinon, qu'est-ce qui est faux?
Merci.
Je ne sais pas. Quel est l'intérêt que ce soit juste ou faux si tu n'aboutis pas ?
amicalement,
e.v.
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 22 Mar 2012, 16:12
Je pensais utiliser le fait que :
 \, = \, n.B_{n-1}(X) \, \Longrightarrow \, B_n(X) \, = \, (\bigint n.B_{n-1}(X)dX))
Or :
dX \, = \, \bigint n.(\bigsum_{k=0}^{n-1} \binom {n-1}k b_k X^{n-1-k}) dX \, = \, \bigsum_{k=0}^{n-1} n \binom {n-1}k b_k X.\frac{X^{n-k}}{n-k} = \bigsum_{k=0}^{n-1} \binom nk b_k X^{n-k+1})
Est-ce une bonne piste? Comment poursuivre?
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
par ev85 » 22 Mar 2012, 17:59
Deluxor a écrit:Je pensais utiliser le fait que :
Or :
Est-ce une bonne piste? Comment poursuivre?
Au risque de me répéter, as-tu songé à la formule de Taylor ? elle te donne les
}(0))
en fonction (très simple) des
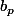
e.v.
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 22 Mar 2012, 18:15
J'arrive donc à :
}(0) \, = \, \frac{n!}{(n-k)!}.b_k.X^n)
Que faut-il faire?
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
par ev85 » 22 Mar 2012, 18:17
Deluxor a écrit:J'arrive donc à :
Que faut-il faire?
Enlever le
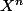
parbleu !
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 22 Mar 2012, 18:31
ev85 a écrit:Enlever le
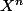
parbleu !
Ah bon?
 \, = \, \bigsum_{k=0}^{n} \frac{n!}{k!(n-k)!}.b_k.X^{n-k} \, = \, \bigsum_{k=0}^{n} \frac{B_n^{(k)}(0)}{k!}.X^k)
D'où :
}(0)}{k!}.X^k \, = \, \frac{n!}{k!(n-k)!}.b_k.X^{n-k})
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
par ev85 » 22 Mar 2012, 18:37
Deluxor a écrit:Ah bon?
D'où :
Ah, je comprends mieux !
ça ne te gène pas d'avoir un polynôme constant égal à un polynôme de degré n ?
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 22 Mar 2012, 18:40
ev85 a écrit:Ah, je comprends mieux !
ça ne te gène pas d'avoir un polynôme constant égal à un polynôme de degré n ?
Si en effet, je trouvais cela étrange.
D'où vient mon erreur?
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
par ev85 » 22 Mar 2012, 18:47
Deluxor a écrit:Si en effet, je trouvais cela étrange.
D'où vient mon erreur?
tes deux sommes
 \, = \, \bigsum_{k=0}^{n} \frac{n!}{k!(n-k)!}.b_k.X^{n-k} \, \textrm{ et } \, \bigsum_{k=0}^{n} \frac{B_n^{(k)}(0)}{k!}.X^k)
ne vont pas dans le même sens. L'une dans celui des degrés décroissants et l'autre dans celui des degrés croissants.
Tu dois égaler les termes de mêmes degré, pas ceux qui se présentent en même temps au guichet.
e.v.
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 22 Mar 2012, 18:57
D'accord, donc on trouve :
}(0) \, = \, b_k.\frac{n!}{(n-k)!})
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
par ev85 » 22 Mar 2012, 19:30
Deluxor a écrit:D'accord, donc on trouve :
Pas d'accord. Tu as supprimé le
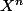
intempestif, mais tu n'as pas égalé les coefficients de mêmes degrés. Ecris une des deux sommes avec le changement d'indice
.
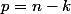
e.v.
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 23 Mar 2012, 20:57
 \, = \, \bigsum_{k=0}^{p+k} \, \frac{(p+k)!}{(n-p)!p!}.b_{n-p}.X^p ?)
Ca me paraît bizarre... je ne vois pas, vraiment.
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
par ev85 » 23 Mar 2012, 21:00
Deluxor a écrit:Ca me paraît bizarre... je ne vois pas, vraiment.
Et pour cause ! k n'est pas défini ! Donc remplace tes deux p+k intempestifs par des n, plus sobres et surtout parfaitement définis.
e.v.
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 23 Mar 2012, 21:36
 \, = \, \bigsum_{k=0}^{n} \, \frac{n!}{(n-p)!p!}.b_{n-p}.X^p)
?
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
par ev85 » 23 Mar 2012, 21:45
Deluxor a écrit: ?
C'est mieux. Maintenant, un petit tour de passe-passe. Tu changes p en k.
e.v.
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
par Deluxor » 23 Mar 2012, 21:58
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités
