Pôlynomes de Lagrange

[youyou2]

Bonjour, je suis entrain de faire un devoir et je bloque à une question sur le polynôme de Lagrange.

1)
a) Vérifier que l'expression du pôlynome d'interpolation de Lagrange pour la fonction f(x)=sin(pix/2), construit sur les points -1; -1/2; 1/2; 1est p(x)=-9x^3/16 + 25x/16

b) En déduire une expression approchée de sin(pi/4) et comparer avec la valeur exacte ;)(2)/2

c) Comparer de même p(2/3) et sin(pi/3)

Je ne sait pas ce qu'il faut faire pour b et c. Pour a, c'est ok

Merci beaucoup :briques:

[Clise]

Bonsoir,

p n'est il pas une approximation de f ?

[youyou2]

Bonsoir,

p n'est il pas une approximation de f ?

P est bien une approximation de f, enfin je crois!

[Clembou]

Bonjour, je suis entrain de faire un devoir et je bloque à une question sur le polynôme de Lagrange.

1)
a) Vérifier que l'expression du pôlynome d'interpolation de Lagrange pour la fonction f(x)=sin(pix/2), construit sur les points -1; -1/2; 1/2; 1est p(x)=-9x^3/16 + 25x/16

b) En déduire une expression approchée de sin(pi/4) et comparer avec la valeur exacte (2)/2

c) Comparer de même p(2/3) et sin(pi/3)

Je ne sait pas ce qu'il faut faire pour b et c. Pour a, c'est ok

Merci beaucoup :briques:

Soit

approxime la fonction

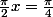
aux points . On veut une valeur approchée de . Que vaut dans l'équation , après faut le remplacer dans ton polynôme. Pareil pour les autres valeurs de la question c)

[Clise]

donc du coup pour trouvé une approximation de sin(pi/4) = f(1/2), tu fais ???

[youyou2]

Soit

approxime la fonction

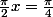
aux points . On veut une valeur approchée de . Que vaut dans l'équation , après faut le remplacer dans ton polynôme. Pareil pour les autres valeurs de la question c)

Donc x=1/2 et on le remplace dans p(x)
p(1/2)= 391/128

Mais si je le compare avec (2)/2, je ne trouve pas la même chose?

[Clise]

oui, c'est normal, c'est une approximation, tes deux fonctions ne sont pas égales !
Tu peux estimer l'erreur en faisant f(1/2) - p(1/2)
ta fonction à construite sert à approximer f par un polynome, ce qui peut être utile.

[youyou2]

J'ai fait une erreur!
p(1/2) = 91/128, et ça fait environ : 0.7109

Et ;)(2)/2= 0.7071

La c'est mieux!

Qu'est ce que je peut dire si je compare les deux valeurs?
qu'elle sont très proche, il y a une erreur de 0.5% environ.

[Clise]

oui, fait de même pour la question c et c'est bon ^^

[youyou2]

Merci beaucoup pour cette aide!

J'ai une 2éme question :

2)
a) Donner un algorithme de calcul de P(x) puis écrire le programme MATLAB qui calcul n valeurs du polynôme d'interpolation de la fonction f, construit sur n points.

b) Faire un graphique de f et de polynôme

[youyou2]

Personne?! :cry:

[Clise]

Qu'est ce que tu ne comprends pas ?

[Clembou]

Merci beaucoup pour cette aide!

J'ai une 2éme question :

2)
a) Donner un algorithme de calcul de P(x) puis écrire le programme MATLAB qui calcul n valeurs du polynôme d'interpolation de la fonction f, construit sur n points.

b) Faire un graphique de f et de polynôme

a) En fait tu dois trouver les de ton polynome d'interpolation. Ton système linéaire à résoudre et le suivant :



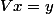
où est la matrice de Vandermonde, , le vecteur des coefficients de ton polynôme et , les valeurs de la fonction aux points d'interpolation...