Salut,
0) L'énoncé est incomplet : il faut
absolument préciser que les xi (i de 0 à n) sont des réels
distincts.
1) Faux : les Li sont tous de degré n-1.
(si la notation te semble obscure, écrit bien proprement qui sont L0, L1 et L2 dans le cas où n=2, histoire de voir de quoi il retourne)
2) et 3) O.K.
4) A mon sens, il y a un "petit piège" dans l'énoncé : on ne te demande pas de "calculer explicitement" les lambda_j, mais juste d'en
donner une expression...
Et sachant que la formule du 3) est vrai
pour tout polynôme P, tu as pas une petite idée de quel(s) polynômes choisir pour avoir directement une expression de lambda_i ?
Concernant la 5), je vois pas trop où ils veulent en venir : il suffit de regarder le polynôme L_i pour voir que son terme de plus haut degré, c'est

où
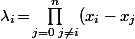)
