Bonjour on me donne ce polynôme:
Pn= (x²-1)^n
On me demande le degré, ses racines et leur ordre de multiplicité.
le degré: 2n+1 mais je ne sais pas le démontré c'est juste logique
racines: 1 et -1 car (x²-1)=(x-1)(x+1) bonne rédaction?
et l'odre de multiplicité c'est n pour les deux.
J'ai bon?
Polynômes juste un oeil
11 messages
- Page 1 sur 1
par normo » 17 Jan 2007, 17:08
ma logique me fait défaut alors, mais pourtant je suis pas convaincu...
par maturin » 17 Jan 2007, 17:17
ben pour connaitre le plus haut degré tu ne t'interesse qu'aux termes de plus haut degré don entre le x² et le 1 tu ne t'interesse qu'au x² et x²^n=x^(2n)
sinon le produit de 2 polynome est un polynome dont le degré est la somme des degré de chaque polynome. Là tu as n produits de polynome de degré 2 donc ça te fera 2+2+2+2....+2 n fois c'est à dire 2n
après tu peux aussi écrire^n=(x-1)^n(x+1)^n)
tu vois donc que ça te donne 2n facteurs de degré 1 donc tu retrouves tes 2n
et en plus ça te donne l'ordre des racines 1 et -1
sinon le produit de 2 polynome est un polynome dont le degré est la somme des degré de chaque polynome. Là tu as n produits de polynome de degré 2 donc ça te fera 2+2+2+2....+2 n fois c'est à dire 2n
après tu peux aussi écrire
tu vois donc que ça te donne 2n facteurs de degré 1 donc tu retrouves tes 2n
et en plus ça te donne l'ordre des racines 1 et -1
par normo » 17 Jan 2007, 17:29
on me donne aussi Ln=Pn^(n) ac Pn=(x²-1)^n
et on me demande Ln(1) et Ln(-1) ça fait 1 et 0?
et on me demande Ln(1) et Ln(-1) ça fait 1 et 0?
par maturin » 17 Jan 2007, 17:45
non 1²-1=0 et 0^n=0
de mêm (-1)²-1=0 et 0^n est toujours égal à 0
la seule forme indeterminée c'est quand n=0
de mêm (-1)²-1=0 et 0^n est toujours égal à 0
la seule forme indeterminée c'est quand n=0
par normo » 17 Jan 2007, 17:52
on me demande ensuite de développer Pn avec la formule du binôme et de trouver ln(x)=n! sigma(a<=k<=n/2) (-1)^k(k parmis n)(n parmis 2n-2k) X^(n-2k)
(désolé pour la présentation)
(désolé pour la présentation)
par maturin » 18 Jan 2007, 11:10
bon j'ai l'impression d'avoir raté un truc Ln=Pn^(n) ça veut dire dérivée nième de Pn ?
moi j'ai considéré que c'était une puissance nième de Pn dans le calul de Ln(1) et de Ln(-1)
hors la formule que tu donne correspond plus à la dérivée.
Donc si on reprend=(x^2-1)^n=(x-1)^n(x+1)^n)
Pour calculer Ln(1) et Ln(-1) il faut considérer la formule^n(x+1)^n)
.
Tu trouve assez rapidement par récurence la dérivée nième d'un produit:
^{(n)}=\sum_{k=0}^n u^{(n-k)}{v^{(k)})
donc si tu prends^n)
et 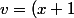^n)
Sachant que la dérivée nieme de^p)
est (p-2)...(p-n+1)(x-a)^{p-n}=n! C_n^p (x-a)^{p-n})
si 
et elle est nulle si pn/2. C'est à dire que seuls les cas )
nous interessent (E()=partie entière)
On a donc}(x)=\sum_{k=0}^{E(\frac{n}{2})} C_{n}^k n! C_n^{2(n-k)}x^{n-2k} (-1)^{k})
moi j'ai considéré que c'était une puissance nième de Pn dans le calul de Ln(1) et de Ln(-1)
hors la formule que tu donne correspond plus à la dérivée.
Donc si on reprend
Pour calculer Ln(1) et Ln(-1) il faut considérer la formule
Tu trouve assez rapidement par récurence la dérivée nième d'un produit:
donc si tu prends
Sachant que la dérivée nieme de
On a donc
par fahr451 » 18 Jan 2007, 11:30
à la pointe de son épée d 'un L qui voulait dire Legendre
famille de polynômes orthogonaux ayant toutes leurs racines (simples) dans ]-1,1[
famille de polynômes orthogonaux ayant toutes leurs racines (simples) dans ]-1,1[
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :