DM Polynomes et complexes

[Rockleader]

Bonsoir à tous, je me prends à l'avance pour préparer ce DM ainsi que le contrôle qui va suivre. Pour tout vous dire, je suis complètement largué pour le moment là dessus, non pas que je ne sois pas capable de comprendre, mais que je n'arrive pas à coller à la méthode d'enseignement de mon prof de math cette année.


Bref...pour commencer voilà le premier exercice:

Déterminer les racines du polynome:




En déduire que:




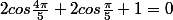
Utiliser cette égalité pour montrer que : est une racine du polynome 4X²+2X-1.


Démontrer que :



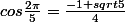
Voilà, il reste d'autres exercice, mais je vais d'abord m’attarder sur celui ci.

Merci pour votre aide.

[wserdx]

Hum, suppose que tu connais les racines d'un polynôme .
Quels sont alors les racines de où est une constante ?
Développe alors et conclus.

[acoustica]

Bonsoir à tous, je me prends à l'avance pour préparer ce DM ainsi que le contrôle qui va suivre. Pour tout vous dire, je suis complètement largué pour le moment là dessus, non pas que je ne sois pas capable de comprendre, mais que je n'arrive pas à coller à la méthode d'enseignement de mon prof de math cette année.


Bref...pour commencer voilà le premier exercice:

Déterminer les racines du polynome:




En déduire que:




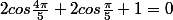
Utiliser cette égalité pour montrer que : est une racine du polynome 4X²+2X-1.


Démontrer que :



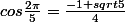
Voilà, il reste d'autres exercice, mais je vais d'abord m’attarder sur celui ci.

Merci pour votre aide.

Re-coucou Rockleader, chacun son tour =)

Tu as un polynôme symétrique de degré 4. Il y a une méthode générale pour calculer les racines de ce genre de polynôme. Exemple :

X^2-5*X-8-5/X+1/X^2=0 en divisant par X^2 après avoir vérifié que X=0 n'était pas solution.

On pose Y:=X+(1/X)(=(X+1)/X) c'est la première forme qui nous intéresse.

On obtient :

(Y^2-2)-5Y-8=0

Y^2-5Y-10=0

Y=(5+/-sqrt(65))/2=(X+1)/X

X*[(5+/-sqrt(65))/2]=X+1

X=2/[3 +/- sqrt(65)]. >>

Magique. =) C'est le même principe avec ton polynôme !

[Rockleader]

Hum, suppose que tu connais les racines d'un polynôme .
Quels sont alors les racines de où est une constante ?
Développe alors et conclus.

Et bien "a" serait une racine de (x-a) donc pour trouver les racines de P il me faudrait le factoriser mais je vois pas trop par quoi =)

Re-coucou Rockleader, chacun son tour =)

Lol merci, content que tu es trouvé l'expression de ta fonction c'est vrai que j'avais pas pensé à la racine carré =)



Je suis pas sur d'avoir très bien compris ta démarche, je regarderais ça quand j'aurais le temps et pas en vitesse 5 minute avant de partir en cours =)

[Sylviel]

wsderx supposait que tu connaissais les racines de P.

Prenons la démarche dans l'autre sens :
trouve les racines de (X-1)P(X), et déduis-en les racines de P(X).

[chan79]

Bonsoir à tous, je me prends à l'avance pour préparer ce DM ainsi que le contrôle qui va suivre. Pour tout vous dire, je suis complètement largué pour le moment là dessus, non pas que je ne sois pas capable de comprendre, mais que je n'arrive pas à coller à la méthode d'enseignement de mon prof de math cette année.


Bref...pour commencer voilà le premier exercice:

Déterminer les racines du polynome:




En déduire que:




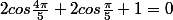
Utiliser cette égalité pour montrer que : est une racine du polynome 4X²+2X-1.


Démontrer que :



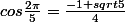
Voilà, il reste d'autres exercice, mais je vais d'abord m’attarder sur celui ci.

Merci pour votre aide.

salut
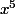
(x;)+x³+x²+1)(x-1)= -1
les racines cherchées sont donc les 4 racines cinquièmes de 1 différentes de 1:
, , ,
la première vérifie x;)+x³+x²+1=0 donc

soit

soit

Corrige ton énoncé, il manque un 2

[Rockleader]

Mais, ce que je ne comprend pas c'est pourquoi vous rajouter tous un (x-1) en facteur du polynôme.



1 est une racine de (x-1)P(x) mais ça m'aide pas plus que ça pour trouver les racines de P non ?

Je cherche surtout à comprendre les méthodes à appliquer pour répondre à ce genre d'exo.

[chan79]

Mais, ce que je ne comprend pas c'est pourquoi vous rajouter tous un (x-1) en facteur du polynôme.



1 est une racine de (x-1)P(x) mais ça m'aide pas plus que ça pour trouver les racines de P non ?

Je cherche surtout à comprendre les méthodes à appliquer pour répondre à ce genre d'exo.

c'est pour pouvoir dire que les racines de ton polynôme sont celles de excepté 1
ce sont donc les quatre racines cinquièmes de l'unité que j'ai écrites plus haut

[Rockleader]

c'est pour pouvoir dire que les racines de ton polynôme sont celles de excepté 1
ce sont donc les quatre racines cinquièmes de l'unité que j'ai écrites plus haut

Ah daccord tout s'éclaire, je pensais que cela changeait le polynome mais puisqu'on ne compte pas la racine de x-1 qui est 1 on peut effectivement dire ça, à partir de là je vois d'où viennent les autres expressions aussi enfin je pense.

Je regarderais tout ça au calme une fois rentré chez moi ce soir et je vous dis si j'ai compris.


Une question tout de même, c'est la méthode générale à appliquer pour ce genre de question ? Multiplier le polynome par x-1 afin d'exprimer les racines n-ième de l'unité ? Ou bien ce n'est possible que parce que l'on est dans un cas particulier ?

Merci à tous.

[chan79]

Ah daccord tout s'éclaire, je pensais que cela changeait le polynome mais puisqu'on ne compte pas la racine de x-1 qui est 1 on peut effectivement dire ça, à partir de là je vois d'où viennent les autres expressions aussi enfin je pense.

Je regarderais tout ça au calme une fois rentré chez moi ce soir et je vous dis si j'ai compris.


Une question tout de même, c'est la méthode générale à appliquer pour ce genre de question ? Multiplier le polynome par x-1 afin d'exprimer les racines n-ième de l'unité ? Ou bien ce n'est possible que parce que l'on est dans un cas particulier ?

Merci à tous.

le polynôme donné est bien particulier; c'est pour ça que ça marche

[Carpate]

c'est pour pouvoir dire que les racines de ton polynôme sont celles de excepté 1
ce sont donc les quatre racines cinquièmes de l'unité que j'ai écrites plus haut

Sans rien rajouter et sans aucune astuce :
est la somme des 5 premiers termes de la suite géométrique de premier terme 1 et de raison x

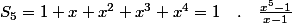
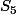
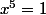
n'est définie que sur R privé de 1 donc les racines de sont les racines de différentes de 1. Ce sont les 4 racines cinquièmes complexes de l'unité (la première : 1 étant réelle).

[Rockleader]

Pour la seconde partie de la question;

EN supposant que cos 2pi/5 est une racine, alors, on devrait pouvoir retrouver avec
Le discriminant qui vaut 2²-4*4*1 = -12

Donc les racines de ce polynomes sont

-4 (+ ou -) racine de 12i /8 = -1+ou-racine de 3i/2 mais je trouve pas ce que je devrais trouver...



Par ailleurs avant ça, il faut quand même démontrer que cos 2pi/5 est une racine de 4x²+2x-1 et là non plus je vois pas trop comment faire

[chan79]

Pour la seconde partie de la question;

EN supposant que cos 2pi/5 est une racine, alors, on devrait pouvoir retrouver avec
Le discriminant qui vaut 2²-4*4*1 = -12

Donc les racines de ce polynomes sont

-4 (+ ou -) racine de 12i /8 = -1+ou-racine de 3i/2 mais je trouve pas ce que je devrais trouver...



Par ailleurs avant ça, il faut quand même démontrer que cos 2pi/5 est une racine de 4x²+2x-1 et là non plus je vois pas trop comment faire

le discriminant est 4+4*4=20

[Rockleader]

le discriminant est 4+4*4=20

AH oui, suis je bête...


DU coup, en racine on a:





ET donc voilà la valeur de cos 2pi/5 car racine du polynome : mais je bloque toujours avant cette question pour démontrer que cos 2pi/5 est bien une racine...peut être en me servant de l'éqquation de départ,, en remplaçant les X par chaque racine de l'unité et en regardant ce que j'obtiens et en essayant de le retraduire en polynome ?

[Rockleader]

Des idées ?

[chan79]

AH oui, suis je bête...


DU coup, en racine on a:





ET donc voilà la valeur de cos 2pi/5 car racine du polynome : mais je bloque toujours avant cette question pour démontrer que cos 2pi/5 est bien une racine...peut être en me servant de l'éqquation de départ,, en remplaçant les X par chaque racine de l'unité et en regardant ce que j'obtiens et en essayant de le retraduire en polynome ?

on a démontré au début que cos(2pi/5) était une racine solution de 4x²+2x-1=0
Ecris ces deux solutions et pense que cos(2pi/5) est positif
J'espère que tu as corrigé les erreurs de l'énoncé:
Il fallait lire:



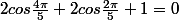
Utiliser cette égalité pour montrer que : est une racine du polynome 4X²+2X-1.


Démontrer que :

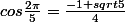
[Doraki]

T'as montré que 2cos(4;)/5)+2cos(2;)/5)+1 = 0 ?

[Rockleader]

T'as montré que 2cos(4;)/5)+2cos(2;)/5)+1 = 0 ?

Oui, je l'ai fais. C'est pour la suite que je coince.

J'espère que tu as corrigé les erreurs de l'énoncé:

Oui j'ai bien vu, c'était une erreur de frappe de ma part.

on a démontré au début que cos(2pi/5) était une racine solution de 4x²+2x-1=0

On ne l'a pas démontré puisque on me demande de le démontrer et que c'est là que je coince

[Doraki]

Saurais-tu exprimer cos(4;)/5) en fonction de cos(2;)/5) ?

[Rockleader]

Saurais-tu exprimer cos(4;)/5) en fonction de cos(2;)/5) ?

cos(4pi/5) = cos(2pi/5 + 2pi/5) = cos(2pi/5)cos(2pi/5) - sin(2pi/5)sin(2pi/5) = cos²(2pi/5) - sin²(2pi/5) = 1 (pas sur du =1) mais je vois pas vraiment à quoi cela m'avance...