DM Polynomes et complexes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Rockleader
- Habitué(e)
- Messages: 2126
- Enregistré le: 11 Oct 2011, 18:42
-
par Rockleader » 22 Oct 2012, 10:14
chan79 a écrit:Tu sais que
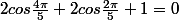
(Egalité 1)
on a la formule
cos 2a = 2cos²a -1
si tu remplaces a par
=2cos^2(\fra{2\pi}{5})-1)
Si on remplace maintenant
)
dans l'égalité 1 ci-dessus, on obtient:
-2 +{2cos}\frac{2\pi}{5}+1=0)
soit
 +{2cos}\frac{2\pi}{5}-1=0)
cela prouve que
est une solution de 4X²+2X-1=0
Erf c'est vrai qu'il y a aussi cette formule là...il y en a tellement que c'est dur de penser toujours à celle dont on a besoin....
Cette histoire est entièrement vraie puisque je l'ai inventé du début à la fin !
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
par fibonacci » 23 Oct 2012, 15:13
Bonjour;
 \\ <br /> \quad \quad = \frac{1}{2}\left( {x_1 + \cos \frac{{6\pi }}{5}} \right)\quad {\rm{pour v\'erifier cette }} \\ <br /> {\rm{relation il faut que l'on ai }} \\ <br /> \frac{1}{2}\left( {x_1 + x_2 } \right) = \frac{1}{2}\left( {x_1 + \cos \frac{{6\pi }}{5}} \right) \to \cos \frac{{6\pi }}{5} = \cos \frac{{4\pi }}{5} \\ <br /> {\rm{d'ou }}\frac{1}{2}\left( {x_1 + x_2 } \right) = x_1 x_2 = - \frac{1}{4} \\ <br /> \end{array})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
