Bonsoir, jaimerais obtenir un peu daide sur lexercice suivant :
On se place dans
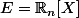
muni du produit scalaire défini par
=\sum_{i=0}^n P(i)Q(i))
1 Pour tout i appartenant à |[0,n]| montrer quil existe un unique polynôme
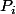
de E tel que :
=\delta_{i,j})
(symboles de Kronecker). Monter que la famille
)
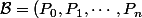est une base orthonormée de E. Pour P appartenant à E, préciser les coordonnées de P dans la base
.
2 Déterminer léquation dans
de lhyperplan
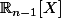
. Montrer que
=n!d(P_0,\mathbb{R}_{n-1}[X]))
où
)
désigne la distance du vecteur x au sous-espace vectoriel H.
3 Ecrire de deux manières
^{2n})
et en déduire la valeur de
.
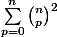
4 Calculer la valeur de
)
Jai fait la question 1 et le début de la question 2 (si vous voyez une erreur, nhésitez pas) :
1 Soit i appartenant à |[0,n]|, supposons quun tel
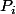
existe.
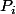
est alors un polynôme de degré inférieur ou égal à n qui possède n racines distinctes (les éléments de |[0,n]| - {i}) donc il existe un réel
tel que
)
.
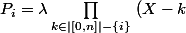Comme
=1)
on a que
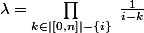
. Doù lunicité. Comme le polynôme trouvé convient, lexistence est immédiate.
Soit j appartenant à |[0,n]| - {i}.
=\sum_{k=0}^n \delta_{i,k}\delta_{j,k}=0)
et
=\sum_{k=0}^n \delta_{i,k}^2=1)
donc
est une base orthonormée de E.
Pour
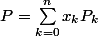
on a
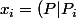=P(i))
2 Soit
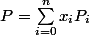
un élément de E. Comme pour tout i de |[0,n]| le coefficient dominant de
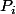
est
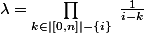
, il en découle que le coefficient dominant de P est
})
.
Comme
=(-1)^{n-i}i!(n-i)!)
(si mes calculs sont corrects
), il en découle que
^{n-i}i!(n-i)!}=0)
, ce qui est aussi équivalent à
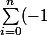^{n-i}{n \choose i}x_i=0)
Je suis bloqué à partir de là, pour ce qui concerne légalité sur les distances. Jai essayé de déterminer le projecteur orthogonal sur
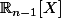
mais je nai pas réussi à aboutir (enfin je suppose que je faisais fausse route puisquon me demande une égalité entre des distances et non pas la valeur dune distance). Les seules informations que jai trouvées potentiellement intéressantes sont que
)
et
.
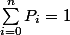
Même chose pour
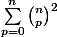
, je connais une méthode avec la dérivée n-ième de
^n)
mais là...
Merci davance.
