Polynome
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
rafbh
- Membre Relatif
- Messages: 250
- Enregistré le: 19 Nov 2006, 17:07
-
 par rafbh » 10 Fév 2008, 16:51
par rafbh » 10 Fév 2008, 16:51
Jai pas envi de trop calculer.
Ca change en fontion de n mais la relation sera aussi en fonction de n.
Tu vois ce que je veux dire?
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 10 Fév 2008, 16:58
par zelda007 » 10 Fév 2008, 16:58
Oui je vois comment faire j'ai essayer jusqu'au rang 3 mais ca devient deja immense et je ne vois pas de relation apparaitre...
Mais tans pis, merci quand meme.
Si quelqu'un veut continuer qu'il n'hesite pas.
Thanks all
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Fév 2008, 20:02
par yos » 10 Fév 2008, 20:02
Bonsoir.
Ton idée de départ est bonne : développer (1+X)^n et dériver ensuite; on trouve
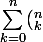\frac{(n+k)!}{k!}x^k)
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 10 Fév 2008, 20:46
par zelda007 » 10 Fév 2008, 20:46
Peux tu détailler car je ne comprends pas du tout comment vous faites...
Et au fait c'est pas (1 + X)^n mais c'est (X + X²)^n
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Fév 2008, 21:51
par yos » 10 Fév 2008, 21:51
^n=X^n\sum_{k=0}^n (_k^n)X^k = \sum_{k=0}^n (_k^n)X^{n+k})
et tu dérives n fois :
^{(n)}=\frac{(n+k)!}{k!}X^k)
.
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 10 Fév 2008, 22:13
par zelda007 » 10 Fév 2008, 22:13
Ok sauf que je ne retrouve pas le meme résultat que avec l'autre méthode.
Le premier resultat trouvé etait :
somme(k parmi n).(n!/k!).X^k.[n!/(n - k)!].[1 + X]^n-k
= somme(k parmi n)².X^k.[1 + X]^n-k.n!
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Fév 2008, 22:16
par yos » 10 Fév 2008, 22:16
zelda007 a écrit:sauf que je ne retrouve pas le meme résultat que avec l'autre méthode.
En apparence.
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 10 Fév 2008, 22:17
par zelda007 » 10 Fév 2008, 22:17
car en vrai c'est pareil ?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 10 Fév 2008, 22:48
par yos » 10 Fév 2008, 22:48
Sauf erreur.
-
zelda007
- Membre Relatif
- Messages: 164
- Enregistré le: 30 Déc 2007, 15:04
-
 par zelda007 » 10 Fév 2008, 22:51
par zelda007 » 10 Fév 2008, 22:51
bon ok merci.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
