Polynome
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
 par antoine 7577 » 20 Fév 2007, 12:22
par antoine 7577 » 20 Fév 2007, 12:22
bonjour j ai un probleme sur cette exercice
Déterminer a et b telle que (X^2-a)*(X^2-b) soit divisible par (X-a)*(X-b)
voila ce que j ai fait : soit A(X)=(X-a)*(X-b)
on veut A(X^2)=Q(X)*A(X) ou Q est un polynome de degres 2
donc Q(X)=cX^2+dX+e
je devellope le produit pour identifier ou je trouve
abe=ab
dab-(b+a)=0
e-d(b+a)=b+a
c=1
-(b+a)+d=0
par identification e=c=1 et d=b+a. Je pense alors resoudre une equation du second degres mais je n en suis pas sur? Y a t il une autre methode plus simple?
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 20 Fév 2007, 12:33
par yos » 20 Fév 2007, 12:33
(X^2-b))
est divisible par
(X-b))
si et seulement si a et b sont racines de
(X^2-b))
.
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 20 Fév 2007, 12:36
par aviateurpilot » 20 Fév 2007, 12:36
soient
=(x^2-a)(x^2-b))
et
=(x-a)(x-b))
si
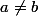
|p(x))
=p(b)=0)
(

ou
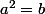
) et (

ou

)
et tu peut continuer mtn...
si

; on aura
=(x^2-a)^2)
et
=(x-a)^2)
|p(x))
=0)
et
=4a(a^2-a)=0)

et (

ou

)
et tu peut continuer mtn...
 par antoine 7577 » 20 Fév 2007, 12:55
par antoine 7577 » 20 Fév 2007, 12:55
okay merci je vien de comprendre (j etait partie beaucoup tro loing).
 par antoine 7577 » 23 Fév 2007, 01:15
par antoine 7577 » 23 Fév 2007, 01:15
bonjour j ai une nouvelle question qui est quasiment identique
je dois desormais determiner a et b pour que A(X) divise A(X^3)
j utilise le meme proceder seulement je dois par la suite montrer que si A(X) est un de ces polynome alors A(-X) en est un aussi et je n y arrive pas .Comment faire.
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 23 Fév 2007, 08:39
par fahr451 » 23 Fév 2007, 08:39
bonjour
soit A solution
A(X^3) = A(X)B(X)
en évaluant en a on obtient
A(a^3) = 0 donc a^3 = a ou a^3 = b
idem pour b
résoudre en a et b
donc A = X^2 ou X(X-1) ou X(X+1) ou (X-1)^2 ou (X+1)^2 ou (X-1)(X+1)
on vérifie que ce sont bien des solutions.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
