Bonsoir, je bloque sur un exo et j’ai besoin de votre aide
Je dois montrer que si X-1 divise le polynôme P(X^n) alors (X^n)-1 divise aussi P(X^n)
Merci
Polynôme
8 messages
- Page 1 sur 1
Re: Polynôme
par pascal16 » 21 Jan 2019, 09:43
je serais bien passé par le fait que toutes les dérivées jusqu'à l'ordre n sont nulles pour X=1, mais j'ai des doutes
Re: Polynôme
par LB2 » 21 Jan 2019, 11:55
Bonjour,
1 est racine de P (pourquoi?)
On sait factoriser X^n-1 et il est à racines simples, dont pour montrer que X^n-1 divise P(X^n), il suffit de montrer que toute racine de X^n-1 est racine de P(X^n), et avec ce qui est dit plus haut cela ne devrait pas poser de problème.
1 est racine de P (pourquoi?)
On sait factoriser X^n-1 et il est à racines simples, dont pour montrer que X^n-1 divise P(X^n), il suffit de montrer que toute racine de X^n-1 est racine de P(X^n), et avec ce qui est dit plus haut cela ne devrait pas poser de problème.
Re: Polynôme
par Ben314 » 21 Jan 2019, 12:12
Salut,
Je sais pas trop à quoi vous jouez avec vos "racines de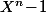
".
L'énoncé dit que\!=\!(X\!-\!1)Q_1(X))
pour un certain 
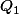donc \!=\!P(1^n)\!=\!0)
ce qui prouve que \!=\!(X\!-\!1)Q_2(X))
pour un certain 
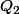et donc que \!=\!(X^n\!-\!1)Q_2(X^n))
.
Je sais pas trop à quoi vous jouez avec vos "racines de
L'énoncé dit que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Polynôme
par LB2 » 21 Jan 2019, 14:09
@Ben Oui tout à fait, j'y ai pensé mais je ne sais pas si la substitution de X^n à X est très claire pour OnePunchMan
Re: Polynôme
par pascal16 » 21 Jan 2019, 20:53
j'étais parti sur (X-1)^n, alors forcément, ça collait pas.
Re: Polynôme
par rcompany » 22 Jan 2019, 17:08
Ou comme pour d'autres problèmes du type P(X)=f(Q(X)) on écrit les polynômes sous la forme de sommes de monômes et l'on résoud un système de (n+1) équations (pour P de degré n)
=\sum_{i=0}^n a_iX^{i}\;\;\;Q(X)=\sum_{i=0}^{n-1} b_iX^{i})
On trouve que pour que=(X-1)Q(X))
, P e Q sont de la forme:
=(-\sum_{i=0}^{n-1} a_i)X^n+\sum_{i=0}^{n-1}a_i X^{i})
et =\sum_{i=0}^{n-1} -(\sum_{k=0}^{i} a_k)X^{n})
car=(X-1)Q(X)=b_{n-1} X^n -b_0 +\sum_{i=1}^{n-1} (b_{i-1}-b_{i})X^{i} \Rightarrow \left \{ \begin{array}{c} b_{0}=-a_0 \\b_0-b_1=a_1\\b_1-b_2=a_2\\...\\b_{n-2}-b_{n-1}=a_{n-1}\\b_{n-1}=a_n<br />\end{array} \right .<br /> \Rightarrow \left \{ \begin{array}{c} b_{0}=-a_0 \\ \forall \;\;1\leq i \leq n-1 , \;\;b_i=-\sum_{k=0}^{i} a_k \\b_{n-1}=a_n=-\sum_{k=0}^{n-1} a_k <br />\end{array} \right .)
On a alors=(X-1)Q(X)=a_n X^n +a_0 + \sum_{i=1}^{n-1}a_i X^{i}=(-\sum_{k=0}^{n-1} a_k)X^{n} +a_0 + \sum_{i=1}^{n-1}a_i X^{i}=-a_0 X^n +a_0 +\sum_{i=1}^{n-1} {(a_i-a_i)X^{i} = -a_0 (X^n-1))
On trouve que pour que
car
On a alors
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :