Une racine (même approchée) est un nombre réel,
pas une liste ! Dans l'algorithme que tu as recopié, la liste est celle des approximations successives. On n'a pas besoin de stocker cette liste si on veut juste rendre une valeur approchée de la racine.
L'algorithme de Newton est une méthode itérative. On part d'un réel, normalement pas trop loin de la racine cherchée, puis on applique itérativement la formule que tu as recopié de ton cours.
Il faut que tu choisisse le point de départ de l'algorithme de Newton. Pour ça, il serait bon que tu commences par étudier le tableau de variation du polynôme dont tu cherches une racine, pour avoir une idée d'un choix raisonnable de point de départ (qui peut dépendre du paramètre

de

).
Ensuite, il faut savoir quand t'arrêter. Le

de l'algorithme que tu as emprunté est le nombre d'itérations. Or ce qu'on veut, c'est une précision garantie (à
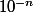
près, où

est donné). Allez, je te donne un tuyau : si

change de signe entre

et

, on est sûr que la racine de

est à une distance de

de moins de
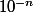
.
A part ça, Newton a droit à une majuscule à son patronyme.

