Bonjour, j’aurais besoin d’aide pour un exercice de mon devoir maison. J’ai réussi les 4 autres mais celui la je n’est pas réussi.
Exercice n°2
l Le plan est muni d’un repere orthonorrné (O; i, j) ,d’unité le centimétre. Soit (p) la
parabole d’équation y = X2 + 2x - 3. On considere la famille de droites (Dm) d’équation y = mx - 2m +5.
1) Verifier que pour tout reel m, A(2; 5) E (Dm) n (p).
2) Etablir une equation du second degré, d’inconnue x, dont les solutions sont les
abscisses des points d’intersection de la droite (Dm) avec la parabole (p).
3) On note f la fonction définie sur R par f(x) = x2 + 2x -3 . Etudier les variations de
et dresser le tableau des variations de f.
4) Déterminer l’unique valeur de m pour laquelle (Dm) et n’ont qu’un point en
comrnun. Tracer (p) et la droite (Dm) correspondante.
Merci beaucoup
Polynome du second degré
11 messages
- Page 1 sur 1
Re: Polynome du second degré
Bonjour
à quelle condition le point A appartient-il à la droite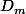 ?
?
à quelle condition le point A appartient-il à la droite
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Polynome du second degré
n = symbole de l'intersection, pas de l'union.
A quel endroit bloques-tu ?
La question 1 : il faut comprendre la question, c'est quelque chose d'inhabituel, donc un peu compliqué. Mais en termes de calculs, c'est hyper simple.
La question 2 : là aussi, la difficulté est de comprendre la question : coment traduire en langage mathématique un truc exprimé en langue française. Et là aussi, il y a très peu de calculs
A quel endroit bloques-tu ?
La question 1 : il faut comprendre la question, c'est quelque chose d'inhabituel, donc un peu compliqué. Mais en termes de calculs, c'est hyper simple.
La question 2 : là aussi, la difficulté est de comprendre la question : coment traduire en langage mathématique un truc exprimé en langue française. Et là aussi, il y a très peu de calculs
Re: Polynome du second degré
l Le plan est muni d’un repère orthonormé ) ,d’unité le centimètre. Soit
,d’unité le centimètre. Soit ) la
la
parabole d’équation . On considère la famille de droites (
. On considère la famille de droites (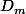 ) d’équation
) d’équation  .
.
1) Vérifier que pour tout réel ,
,  \in (D_m) \cap (P)) .
.
2) Établir une équation du second degré, d’inconnue , dont les solutions sont les
, dont les solutions sont les
abscisses des points d’intersection de la droite) avec la parabole
avec la parabole ) .
.
3) On note f la fonction définie sur par
par  = x^2 + 2x -3) . Étudier les variations de
. Étudier les variations de
et dresser le tableau des variations de .
.
4) Déterminer l’unique valeur de m pour laquelle (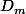 ) et n’ont qu’un point en
) et n’ont qu’un point en
commun. Tracer) et la droite
et la droite ) correspondante.
correspondante.
parabole d’équation
1) Vérifier que pour tout réel
2) Établir une équation du second degré, d’inconnue
abscisses des points d’intersection de la droite
3) On note f la fonction définie sur
et dresser le tableau des variations de
4) Déterminer l’unique valeur de m pour laquelle (
commun. Tracer
Re: Polynome du second degré
Normalement la question 3) ne devrait pas te poser de problèmes (application du cours sur le second degré)
Re: Polynome du second degré
Ok pour le 3).
As tu trouvé la question 2) qui demandait de déterminer l'intersection de P et D_m ?
Tu devrais trouver une équation du second degré en x, dont les coefficients a,b,c dépendent du paramètre m.
Ensuite, une méthode pour la 4) est de remarquer que lorsqu'il y a un seul point dans l'intersection, c'est que l'équation du second degré a une racine double, c'est à dire que Delta = b^2-4ac = 0.
Et tu résous Delta = 0 pour trouver la valeur de m correspondante.
As tu trouvé la question 2) qui demandait de déterminer l'intersection de P et D_m ?
Tu devrais trouver une équation du second degré en x, dont les coefficients a,b,c dépendent du paramètre m.
Ensuite, une méthode pour la 4) est de remarquer que lorsqu'il y a un seul point dans l'intersection, c'est que l'équation du second degré a une racine double, c'est à dire que Delta = b^2-4ac = 0.
Et tu résous Delta = 0 pour trouver la valeur de m correspondante.
Re: Polynome du second degré
Je bon essayer et essayer je trouve pas la solution. J’adore les maths mais la ce chapitre j’aime pas du tout. Je vois pas le résultat que ça pourrait être et mon cours est incompréhensible !
Re: Polynome du second degré
Tu peux écrire tes calculs sur le forum.
Pour l'intersection de P et D_m :
- Soit m fixé.
Le point A de coordonnées (x,y) appartient à P si et seulement si ...
Il appartient à D_m si et seulement si ...
Donc il appartient à l'intersection si et seulement si ...
Pour l'intersection de P et D_m :
- Soit m fixé.
Le point A de coordonnées (x,y) appartient à P si et seulement si ...
Il appartient à D_m si et seulement si ...
Donc il appartient à l'intersection si et seulement si ...
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
