Polynôme orthogonaux
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
cadi
- Membre Naturel
- Messages: 33
- Enregistré le: 16 Mar 2007, 10:02
-
 par cadi » 16 Mar 2007, 11:03
par cadi » 16 Mar 2007, 11:03
bonjour
voici le sujet de la question ou je suis bloquer
Soit

la fontion définie sur

par :
pour tout
 = exp(-t^2))
.
on définie

application de

X

dans

comme suit :
pour
\in (\mathbb{R}[X])^2)
,

integrale de -l'infini à + l'infini de
Q(t)w(t))
j'ai réussi a montrer que
}(t)=(-1)^n H_n(t)w(t))
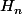
est une suite de polynôme telle que pour tout

, d°

, le coefficient dominant de
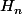
est

il me reste a montrer que pour tout n>1
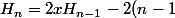H_{n-2})
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 16 Mar 2007, 11:50
par fahr451 » 16 Mar 2007, 11:50
bonjour
on a w '(t) = -2t w(t)
on dérive n-1 fois en utilisant la formule de leibniz
w^(n) (t) = -2t w^(n-1) (t) + (1 parmi n-1) (-2) w^(n-2) (t)
et directement le résultat demandé.
-
cadi
- Membre Naturel
- Messages: 33
- Enregistré le: 16 Mar 2007, 10:02
-
 par cadi » 18 Mar 2007, 21:07
par cadi » 18 Mar 2007, 21:07
fahr451 a écrit:bonjour
on a w '(t) = -2t w(t)
on dérive n-1 fois en utilisant la formule de leibniz
w^(n) (t) = -2t w^(n-1) (t) + (1 parmi n-1) (-2) w^(n-2) (t)
et directement le résultat demandé.
merci de votre aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités