Polynôme et nombres complexes
16 messages
- Page 1 sur 1
Polynôme et nombres complexes
Bonsoir à tous
j'essaye depuis plusieurs heures de résoudre cette question, et je n'y arrive toujours pas...
-on considère dans toute cette partie n nombres complexes a0,...,an-1 et la fonction polynôme P définie par P(z)= Somme (k=0 à n-1) de ak*z^k)
Montrer que: 1/n * Somme (k=0 à n-1) (module²(P((e^2kpi)/n)) = Somme (j=0 à n-1) (module²(aj)
Ce qui m'intrigue c'est qu'il n y a pas de i donc je ne peux pas utiliser les propriétés des complexes, j'ai donc vu le module de P au carré comme P fois son conjugué,mais je n'aboutis à rien...
Merci pour votre aide
j'essaye depuis plusieurs heures de résoudre cette question, et je n'y arrive toujours pas...
-on considère dans toute cette partie n nombres complexes a0,...,an-1 et la fonction polynôme P définie par P(z)= Somme (k=0 à n-1) de ak*z^k)
Montrer que: 1/n * Somme (k=0 à n-1) (module²(P((e^2kpi)/n)) = Somme (j=0 à n-1) (module²(aj)
Ce qui m'intrigue c'est qu'il n y a pas de i donc je ne peux pas utiliser les propriétés des complexes, j'ai donc vu le module de P au carré comme P fois son conjugué,mais je n'aboutis à rien...
Merci pour votre aide
bonjour,
on écrit la définition du membre de gauche de l'égalité
en utilisant trois indices entiers j;k;m . Le conjugué d'une somme est la somme des conjugués
\left( \sum_{m=0}^{n-1} \bar{a_m} e^{-2ijm \frac{\pi}{n}} \right))
par double distributivité de la multiplication sur l'addition, le produit de deux sommes
est la somme des produits
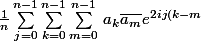 \frac{\pi}{n}})
avec trois sommes, on peut permuter les signes sigma.....tu peux également utiliser les progressions géomètriques (cf L'algèbre discrète de la transformée de Fourier de Gabriel Peyré chez Eyrolles)
on écrit la définition du membre de gauche de l'égalité
en utilisant trois indices entiers j;k;m . Le conjugué d'une somme est la somme des conjugués
par double distributivité de la multiplication sur l'addition, le produit de deux sommes
est la somme des produits
avec trois sommes, on peut permuter les signes sigma.....tu peux également utiliser les progressions géomètriques (cf L'algèbre discrète de la transformée de Fourier de Gabriel Peyré chez Eyrolles)
busard_des_roseaux a écrit:bonjour,
on écrit la définition du membre de gauche de l'égalité
en utilisant trois indices entiers j;k;m . Le conjugué d'une somme est la somme des conjugués
par double distributivité de la multiplication sur l'addition, le produit de deux sommes
est la somme des produits
avec trois sommes, on peut permuter les signes sigma.....tu peux également utiliser les progressions géomètriques (cf L'algèbre discrète de la transformée de Fourier de Gabriel Peyré chez Eyrolles)
oui d'où est-ce que tu sors le i ?
busard_des_roseaux a écrit:
la formule à démontrer est encore plus forte, ça marche sans?, vires-le s'il n'est pas dans l'énoncé.
je ne sais pas s'il y a duou non (avec
).
En général, on utilise
Il n'y a pas de i , et apparemment ce n'est pas une faute de frappe car y a pas de i dans toutes les égalités des questions suivantes... donc du coup je me retrouve avec exp((2j(k+m)*pi)/(n))
le facteur 1/n comment je m'en débarrasse ? comment rendre les deux indices des a égaux ?
on a ceci:
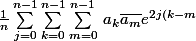 \frac{\pi}{n}})
dans les deux sommes les plus intérieures, on sépare les éléments diagonaux du reste de la somme, ça donne
 \frac{\pi}{n}})
on somme sur j
 \pi}) (1)
(1)
Par hypothèse, la somme (1) est réelle.
Le domaine d'indices est un carré, privé de la diagonale, dont les deux triangles se correspondent
par la symétrie : (k,m)---->(m,k)
je réfléchis :mur:
dans les deux sommes les plus intérieures, on sépare les éléments diagonaux du reste de la somme, ça donne
on somme sur j
Par hypothèse, la somme (1) est réelle.
Le domaine d'indices est un carré, privé de la diagonale, dont les deux triangles se correspondent
par la symétrie : (k,m)---->(m,k)
je réfléchis :mur:
Si tu prends n=2 et P(x) = x, on voit rapidement que ta formule est fausse.
Non seulement tu as mal mis les parenthèses, mais en plus il faut bien un i dans les exposants.
Il faut prendre 1/n * Somme (k=0 à n-1) |P(e^(2ikpi/n))|²
Et cette égalité n'est rien d'autre qu'un avatar du fait que la transformée de Fourier est une isométrie de L².
Si P et Q sont deux polynômes de degré n-1,
Somme des P(;)^k)*Q(;)^-k)
= Somme des (Somme des ai ;)^ki) * (Somme des bj ;)^-kj)
= Somme des aibj ;)^k(i-j)
= Somme des aibj (Somme pour k=0 à n-1 de ;)^k(i-j)).
= Somme des aibj (n si (i-j) est multiple de n, 0 sinon).
= n * Somme des aibi
Tu appliques ça à P et son conjugué, et ça donne l'égalité cherchée.
Non seulement tu as mal mis les parenthèses, mais en plus il faut bien un i dans les exposants.
Il faut prendre 1/n * Somme (k=0 à n-1) |P(e^(2ikpi/n))|²
Et cette égalité n'est rien d'autre qu'un avatar du fait que la transformée de Fourier est une isométrie de L².
Si P et Q sont deux polynômes de degré n-1,
Somme des P(;)^k)*Q(;)^-k)
= Somme des (Somme des ai ;)^ki) * (Somme des bj ;)^-kj)
= Somme des aibj ;)^k(i-j)
= Somme des aibj (Somme pour k=0 à n-1 de ;)^k(i-j)).
= Somme des aibj (n si (i-j) est multiple de n, 0 sinon).
= n * Somme des aibi
Tu appliques ça à P et son conjugué, et ça donne l'égalité cherchée.
busard_des_roseaux a écrit:@hsina: par curiosité, dans quel contexte est donné un énoncé faux , et ce, sur plusieurs questions ?
en effet dans toutes les questions le i n'existe pas dans les exponentielles...après est-ce que le prof a vraiment oublié pour la 1ere et fait copié/collé après, ou bien c'est voulu...
Doraki a écrit:Si tu prends n=2 et P(x) = x, on voit rapidement que ta formule est fausse.
Non seulement tu as mal mis les parenthèses, mais en plus il faut bien un i dans les exposants.
Il faut prendre 1/n * Somme (k=0 à n-1) |P(e^(2ikpi/n))|²
Et cette égalité n'est rien d'autre qu'un avatar du fait que la transformée de Fourier est une isométrie de L².
Si P et Q sont deux polynômes de degré n-1,
Somme des P(;)^k)*Q(;)^-k)
= Somme des (Somme des ai^ki) * (Somme des bj
^-kj)
= Somme des aibj^k(i-j)
= Somme des aibj (Somme pour k=0 à n-1 de^k(i-j)).
= Somme des aibj (n si (i-j) est multiple de n, 0 sinon).
= n * Somme des aibi
Tu appliques ça à P et son conjugué, et ça donne l'égalité cherchée.
je ne comprends pas bien le raisonnement suivi pour passer de 3 sommes à une seule somme
hsina a écrit:en effet dans toutes les questions le i n'existe pas dans les exponentielles...après est-ce que le prof a vraiment oublié pour la 1ere et fait copié/collé après, ou bien c'est voulu...
c'est ce que je pense, le prof a oublié le
hsina a écrit:je ne comprends pas bien le raisonnement suivi pour passer de 3 sommes à une seule somme
bonjour,
je détaille les explications de Doraki
après avoir distribué la multiplication sur l'addition, on trouve
la somme de la progression géométrique d'exposant k, elle vaut 0 , sauf si j=m,dans ce cas elle se calcule directement et vaut
le résultat final est donc
busard_des_roseaux a écrit:bonjour,
je détaille les explications de Doraki
après avoir distribué la multiplication sur l'addition, on trouve
la somme de la progression géométrique d'exposant k, elle vaut 0 , sauf si j=m,dans ce cas elle se calcule directement et vaut
le résultat final est donc
MErci beaucoup pour les précisions, j'avais pas pensé à calculer la somme géométrique dans le cas où m=j
encore merci
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
