Polynome minimal

par **quadrature** » 19 Aoû 2008, 07:29

Bonjour
Je n'arrive pas à trouver la solution pour ce problème

Sachant que p divise q^3 , q² divise 8(p^3) et P/q est une fraction irréductible .
Quelles sont les valeurs possibles de p et q? (réponse p=+/-1, q=+/-1 ou +/-2), mais comment justifier?

Remarque:

L'ojectif de ma démo est de prouver que P(x)=4x^3-3x-1/2 est irréductible dans Q[X] donc ....

par **ThSQ** » 19 Aoû 2008, 07:44

Effectivement P étant de degré 3 il suffit de montrer qu'il n'a pas de racine dans Q.

Si pgcd(p,q)=1 et p | q^3 ça laisse pas des tonnes de possibilités pour p.

par **magnolia86** » 19 Aoû 2008, 11:43

quadrature a écrit:L'ojectif de ma démo est de prouver que P(x)=4x^3-3x-1/2 est irréductible dans Q[X] donc ....

Regarde ton polynôme modulo 5,

, tu verras (en testant les 5 classes

) qu'il n'a pas de racine :zen:

par **ThSQ** » 19 Aoû 2008, 18:59

magnolia86 a écrit:Regarde ton polynôme modulo 5, , tu verras (en testant les 5 classes ) qu'il n'a pas de racine :zen:

C'est pas vraiment plus rapide que de regarder les quelques rationnels potentiellement racines (voire 4p^3+27q^2)

par **ThSQ** » 19 Aoû 2008, 19:02

magnolia86 a écrit:Regarde ton polynôme modulo 5, , tu verras (en testant les 5 classes ) qu'il n'a pas de racine :zen:

C'est pas vraiment plus rapide que de regarder les quelques rationnels potentiellement racines (voire en regardant le discriminant 4p^3+27q^2)

par **magnolia86** » 19 Aoû 2008, 19:03

ThSQ a écrit:C'est pas vraiment plus rapide que de regarder les quelques rationnels potentiellement racines

C'est vrai. :zen:

ThSQ a écrit:(voire en regardant le discriminant 4p^3+27q^2)

là, c'est déjà plus sophistiqué.

par **quadrature** » 20 Aoû 2008, 04:09

merci pour le pistes, mais je n'ai pas encore la réponse :cry:
je crois qu'il faut résonner sur les diviseurs q^3 et 8p^3 avec la condition que p et q sont premiers entre eux on doit pouvoir éliminer les solutions différents de p=+/-1, q=+/-1 ou +/-2 .
Mais j'ai besoin d'une démonstration rigoureuse, je dois expliquer à des Es... :ptdr:

par **quadrature** » 28 Aoû 2008, 12:20

Alors, personne ne veut me répondre, c'est vraiment important pour moi :cry: .
Merci d'avance

par **yos** » 28 Aoû 2008, 13:11

et p premier avec q entraînent p=1 ou -1. C'est le lemme de Gauss.

par **quadrature** » 29 Aoû 2008, 22:26

Merci Yos, y'a-t-il un lien vers ce lemme car j'ai cherché et je trouve des réponses contradictoires.

par **yos** » 30 Aoû 2008, 15:14

Le lemme de Gauss (ou Gauss-Euclide) dit que si

et

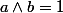
, alors

.

Polynome minimal

polynome minimal

réaction

Qui est en ligne