Bonjour,
Je vous écris car je rencontre un problème avec l'interpolation par morceaux.
f(x)=1/(1+x)
x appartient à I= [0,1].
Pouvez_vous m'aider à trouver un moyen de déterminer le nombre minimal d'intervalles, pour que le polynôme linéaire par morceaux qui interpole la fonction par intervalles donne une erreur <=10^-5?
Bien évidemment, je ne me permet pas de vous demander la solution toute faite, mais dans on a un peu "survolé" cette partie du cours, et j'aimerai avoir votre aide, pour savoir comment m'y prendre.
Merci d'avance,
Polynôme linéaire par morceaux
6 messages
- Page 1 sur 1
Bonsoir,
je n'ai pas fait les calculs mais si tu nommes) la fonction affine qui interpole f sur le sous intervalle
la fonction affine qui interpole f sur le sous intervalle 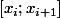 de
de  en
en  et
et 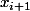 alors puisque f est convexe ce que tu cherches revient à dire que
alors puisque f est convexe ce que tu cherches revient à dire que -f(x)\leq 10^{-5}) pour tout x dans
pour tout x dans 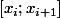 .
.
Tu peux expliciter clairement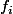 , l'inéquation reviendra alors (après multiplication par (1+x) ) à chercher les valeurs de
, l'inéquation reviendra alors (après multiplication par (1+x) ) à chercher les valeurs de 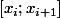 pour lesquels un polynôme du second degré est inférieur à une constante...
pour lesquels un polynôme du second degré est inférieur à une constante...
Il y aura donc une distance maximum entre x et chaque bornes de l'intervalle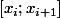 qui ne devra pas être dépassée, il suffira alors de construire
qui ne devra pas être dépassée, il suffira alors de construire 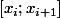 assez petit et la longueur de ce dernier intervalle te permettra de trouver le nombre d'intervalles nécessaire :
assez petit et la longueur de ce dernier intervalle te permettra de trouver le nombre d'intervalles nécessaire : ) (éventuellement +1, E partie entière)
(éventuellement +1, E partie entière)
je n'ai pas fait les calculs mais si tu nommes
Tu peux expliciter clairement
Il y aura donc une distance maximum entre x et chaque bornes de l'intervalle
Bonsoir José,
Je te remercie tout d'abord pour ta réponse on ne peut plus complète, claire et précise.
Seulement, j'ai une question (qui peut paraitre un peu stupide), mais quand tu parles du sous-intervalle [x_i;x_{i+1}] de [0;1], ma question est : comment choisir ce sous-intervalle?
en lisant ton post, je pensais que [x_i;x_{i+1}] devait justement correspondre à l'intervalle [0;1].
Peux-tu m'éclairer sur ce point s'il te plait??
Merci d'avance
Je te remercie tout d'abord pour ta réponse on ne peut plus complète, claire et précise.
Seulement, j'ai une question (qui peut paraitre un peu stupide), mais quand tu parles du sous-intervalle [x_i;x_{i+1}] de [0;1], ma question est : comment choisir ce sous-intervalle?
en lisant ton post, je pensais que [x_i;x_{i+1}] devait justement correspondre à l'intervalle [0;1].
Peux-tu m'éclairer sur ce point s'il te plait??
Merci d'avance
Bonjour,
Salut Tize, :happy2:
en gardant tes notations,
=f(x_i)+\alpha \left( x -x_i \right))
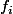 est la fonction affine qui interpole f aux bornes
est la fonction affine qui interpole f aux bornes
de l'intervalle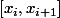
avec-f(x_i)}{x_{i+1}-x_i})
d'après le théorème des accroissements finis,
il existe tel que
tel que )
on pose=f(x) - f_i(x))
 = f'(x) - \alpha=f'(x) -f'(\xi))
=f''(x))
f est convexe, f ' est croissante, f'' est positive,
décroissante, majorée par 2.
 \leq 2)
En intégrant deux fois cette inégalité, on montre que:
| \leq (x_{i+1}-x_i)^2)
On considère une subdivision régulière de [0;1] de pas où n est un entier suffisamment grand:
où n est un entier suffisamment grand:
-f_i(t) \leq n^{-2})
Il suffit donc de prendre pour satisfaire l'inégalité désirée :
pour satisfaire l'inégalité désirée :

Salut Tize, :happy2:
en gardant tes notations,
de l'intervalle
avec
d'après le théorème des accroissements finis,
il existe
on pose
f est convexe, f ' est croissante, f'' est positive,
décroissante, majorée par 2.
En intégrant deux fois cette inégalité, on montre que:
On considère une subdivision régulière de [0;1] de pas
Il suffit donc de prendre
Bonjour,
Merci énormément pour vos éléments de réponse.
On doit donc utiliser la relation Nh= b-a.
Avec l'intervalle [a,b] et N : le nombre minimal d'intervalles, et donc déduire que Nh=1, donc h=1/N, et après, faire le ln pour trouver N.
Je vois désormais ce qu'il faut faire :id:
Encore une fois merci beaucoup!!!
Merci énormément pour vos éléments de réponse.
On doit donc utiliser la relation Nh= b-a.
Avec l'intervalle [a,b] et N : le nombre minimal d'intervalles, et donc déduire que Nh=1, donc h=1/N, et après, faire le ln pour trouver N.
Je vois désormais ce qu'il faut faire :id:
Encore une fois merci beaucoup!!!
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
