Polynome de Legendre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pozor16
- Membre Naturel
- Messages: 34
- Enregistré le: 30 Avr 2006, 17:04
-
 par pozor16 » 01 Mai 2012, 08:51
par pozor16 » 01 Mai 2012, 08:51
Bonjour à tous,
J'aurais besoin d'aide pour résoudre un problème sur les polynomes de Legendre(
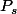
est translaté à l'iintervalle [0,1] et normalisé).
Soit N(x) =
 + aP_{s-1}(x))
où
)
=
!})
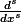
^s))
Je dois montrer que toutes les racines de N(x) sont réelles et distinctes (a étant réelle).
Quelqu'un peut-il me donner une piste?
Merci d'avance

-
Maxmau
- Membre Irrationnel
- Messages: 1149
- Enregistré le: 19 Mar 2008, 10:11
-
 par Maxmau » 01 Mai 2012, 09:54
par Maxmau » 01 Mai 2012, 09:54
pozor16 a écrit:Bonjour à tous,
J'aurais besoin d'aide pour résoudre un problème sur les polynomes de Legendre(
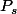
est translaté à l'iintervalle [0,1] et normalisé).
Soit N(x) =
 + aP_{s-1}(x))
où
)
=
!})
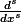
^s))
Je dois montrer que toutes les racines de N(x) sont réelles et distinctes (a étant réelle).
Quelqu'un peut-il me donner une piste?
Merci d'avance

Bj Applique "Rolle' en cascade
-
cdav
- Membre Naturel
- Messages: 27
- Enregistré le: 30 Avr 2012, 08:13
-
 par cdav » 01 Mai 2012, 19:51
par cdav » 01 Mai 2012, 19:51
Maxmau a écrit:Bj Applique "Rolle' en cascade
Soit a1 , a2 , . . . , ap les racines dordres impairs de Ln appartenant à ];)1, 1[.
Soit Q = (X

a1 )(X

a2 ) . . . (X

ap ). La fonction t

Ln (t)Q(t) est continue,
1
de signe constant sur [;)1, 1] sans être la fonction nulle donc

1 Ln (t)Q(t) dt = 0.
Compte tenu de b) on a nécessairement p n puis p = n car le nombre de racines
ne peut excéder n.. De plus les racines a1 , a2 , . . . , an sont simples car la somme de
leurs multiplicités ne peut excéder n.
http://www.ismath.fr
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 28 invités
est translaté à l'iintervalle [0,1] et normalisé).
=
!})