Polynome de legendre
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 11 Déc 2011, 23:06
par bentaarito » 11 Déc 2011, 23:06
bonsoir

pour la dernière question, je vois pas pourquoi on a l'écriture de la 1ere ligne! :hum:
-
JeanJ
- Membre Relatif
- Messages: 264
- Enregistré le: 09 Jan 2010, 09:04
-
 par JeanJ » 12 Déc 2011, 07:45
par JeanJ » 12 Déc 2011, 07:45
Le document joint est illisible.
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 12 Déc 2011, 17:59
par bentaarito » 12 Déc 2011, 17:59
JeanJ a écrit:Le document joint est illisible.
voilà le lien
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 12 Déc 2011, 18:47
par Doraki » 12 Déc 2011, 18:47
A mon avis il faut inventer la définition de Pn de sorte que ça marche.
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 12 Déc 2011, 20:03
par bentaarito » 12 Déc 2011, 20:03
c'est les polynomes de Legendre
j'ai pas mis la définition car j'ai jugé pas nécessaire de l'utiliser dans cette question
( je pense que ça doit découler de la 4/ mais j'y arrive pas )
=\frac{n!}{(2n)!}\frac{\textrm{d}^n}{\textrm{d}x^n}\left((x^2-1)^n\right))
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 12 Déc 2011, 20:04
par bentaarito » 12 Déc 2011, 20:04
ce sont les polynômes de Legendre
=\frac{n!}{(2n)!}\frac{\textrm{d}^n}{\textrm{d}x^n}\left((x^2-1)^n\right))
j'ai pas mis la définition car j'ai jugé pas nécessaire de l'utiliser dans cette question
( je pense que ça doit découler de la 4/ mais j'y arrive pas )
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 12 Déc 2011, 22:27
par bentaarito » 12 Déc 2011, 22:27
alors pas d'idées?
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 13 Déc 2011, 18:18
par bentaarito » 13 Déc 2011, 18:18
up :stupid_in
-
fal
- Membre Naturel
- Messages: 54
- Enregistré le: 16 Déc 2010, 17:34
-
 par fal » 14 Déc 2011, 12:29
par fal » 14 Déc 2011, 12:29
POUR 3) remarque aue (x²-1)puissn =(x-1)puis n *(x+1)puiss n ; et integre par partie; le calcul est penible!!
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 14 Déc 2011, 15:33
par bentaarito » 14 Déc 2011, 15:33
fal a écrit:POUR 3) remarque aue (x²-1)puissn =(x-1)puis n *(x+1)puiss n ; et integre par partie; le calcul est penible!!
la 3/ je l'ai faite et y'a pas de calcul pénible :ptdr: (faut pas faire comme tu suggères :lol3: )
j'ai répondu à toutes les questions ( même la 6/ d'ailleurs!!) mais j'arrive pas à justifier l'écriture donnée dans la 1ere ligne de la 6/
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 14 Déc 2011, 21:07
par bentaarito » 14 Déc 2011, 21:07
personne!!!
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 15 Déc 2011, 16:19
par Pythales » 15 Déc 2011, 16:19
bentaarito a écrit:personne!!!
C'est curieux, car on trouve
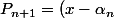P_n-\sum_0^{n-1}\alpha_iP_i)
, et le dernier terme ne se réduit pas à un

Et d'autant plus curieux que la relation de récurrence des polynomes de Lagrange est

Es tu bien sûr que les
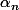
et les
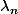
sont des constantes ?
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 15 Déc 2011, 16:52
par Doraki » 15 Déc 2011, 16:52
Et c'est quoi les questions 1 et 2, leur résultat et le résultat de la question 5 ?
Y'a sans doute des histoires de polynômes orthogonaux et de produit scalaires pour montrer que Pn est combinaison linéaire de xP(n-1) et P(n-2).
 par alavacommejetepousse » 16 Déc 2011, 21:33
par alavacommejetepousse » 16 Déc 2011, 21:33
bonsoir il suffit de remarquer que les Pi sont de degré i et unitaires donc (Po,...Pn,xPn) est une base de R(n+1)[X] et Pn+1 se décompose dedans avec 1 comme coordonnée sur xPn
 par alavacommejetepousse » 16 Déc 2011, 21:42
par alavacommejetepousse » 16 Déc 2011, 21:42
bonsoir
on écrit 4) pour xPn et ensuite en faisant les produit scalaires avec les Pi i < n-1
comme Pn+1 ,Pn, xPn orthogonaux à Pi on a le résultat
-
bentaarito
- Membre Rationnel
- Messages: 603
- Enregistré le: 30 Oct 2009, 01:58
-
 par bentaarito » 17 Déc 2011, 14:13
par bentaarito » 17 Déc 2011, 14:13
sauf que moi je parle de la dernière question 6/
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités

