On considère
Qu'obtenez vous en faisant une intégration par partie ? Normalement, le calcul
Polynôme de Legendre - Intégration
7 messages
- Page 1 sur 1
Polynôme de Legendre - Intégration
par Zweig » 30 Mai 2010, 13:10
Salut,
On considère}{1-(1-ax)b}\,dx)
avec a et b des constantes réelles et 
le 
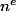
polynôme de Legendre. Si je prends  = P_n(x))
pour faire une intégration par partie, alors  = \frac{P_{n+1}(x) - P_{n-1}(x)}{2n+1})
(http://functions.wolfram.com/PDF/LegendrePGeneral.pdf)
Qu'obtenez vous en faisant une intégration par partie ? Normalement, le calcul}{1-(1-ax)b}\right]^{1}_{0})
devrait donner 0 ... Mais Wolfram me dit le contraire ...
On considère
Qu'obtenez vous en faisant une intégration par partie ? Normalement, le calcul
par ToToR_2000 » 30 Mai 2010, 15:46
Non, je ne crois pas que cela fasse 0. La valeur en 1 de l'expression entre crochets est nulle (P_i(1) =1) mais celle en 0 n'a aucune raison de l'être (d'après les formules sur wiki)
par Zweig » 30 Mai 2010, 16:36
Je remplace la fraction par une fonction 
.
Je prends comme définition de celle-ci : =\frac{1}{n!}\frac{d^n}{dx^n}(x(1-x))^n)
f(x)\,dx = \int\frac{1}{n!}\frac{d^n}{dx^n}(x(1-x))^n\cdot f(x)\,dx = \int\frac{d}{dx}\left[\frac{1}{n!}\frac{d^{n-1}}{dx^{n-1}}(x(1-x))^n\right]\cdot f(x)\,dx)
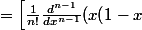)^n\cdot f(x)\right]^1_0 - \int \frac{1}{n!}\frac{d^{n-1}}{dx^{n-1}}(x(1-x))^n\cdot f'(x)\,dx = 0 - \int \frac{1}{n!}\frac{d^{n-1}}{dx^{n-1}}(x(1-x))^n\cdot f'(x)\,dx)
Je prends comme définition de
par ToToR_2000 » 30 Mai 2010, 21:15
Effectivement, avec , on trouve bien que le crochet de l'IPP est nulle.
Cela dit, sur wikipedia
http://fr.wikipedia.org/wiki/Polyn%C3%B4me_de_Legendre
la formule est différente de la tienne auquel cas le crochet n'est plus nul, donc soit il y a plusieurs polynomes de Legendre possibles (pour un n donné), soit l'une des formules est fausse (logique de haut vol :we: )
Cela dit, sur wikipedia
http://fr.wikipedia.org/wiki/Polyn%C3%B4me_de_Legendre
la formule est différente de la tienne auquel cas le crochet n'est plus nul, donc soit il y a plusieurs polynomes de Legendre possibles (pour un n donné), soit l'une des formules est fausse (logique de haut vol :we: )
par Zweig » 31 Mai 2010, 17:18
Bizarre, la formule utilisée sur Wiki ne concorde pas avec celles du PDF ... Perso, je fais plus confiance à Wolfram qu'à Wiki ...
par ToToR_2000 » 31 Mai 2010, 17:41
Je crois que wiki a bon sur ce coup-là:
http://www.sciences.univ-nantes.fr/physique/perso/blanquet/conducti/a1besleg/a1besleg.htm
ça confirme la formule en x^2
http://www.sciences.univ-nantes.fr/physique/perso/blanquet/conducti/a1besleg/a1besleg.htm
ça confirme la formule en x^2
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :