Polynôme d’interpolation de Lagrange

[novicemaths]

Bonsoir



Je cherche le polynôme d’interpolation de Lagrange pour les points
d’appui d’abscisses : −2, −1,0, 1, 2. Sans aucune information des points de y.

J'ai fait y =f(x).











Avant de chercher le polynôme, je souhaiterai savoir si mon raisonnement est correct ?

A bientôt

[GaBuZoMeu]

Bonsoir,
Tu cherches bien à interpoler la fonction en ces 5 points d'interpolation ?
est paire, les points d'interpolation sont situés symétriquement par rapport à l'origine. Inutile de s'embêter avec Lagrange, le polynôme d'interpolation est pair de degré inférieur ou égal à 4, le terme constant s'obtient immédiatement et il ne reste plus que deux coeffcients à déterminer ....

[novicemaths]

Donc, j'ai faux.

Le but de l'exercice est de tracer f et de tracer le polynôme d’interpolation avec des points
d’appui d’abscisses.

Les deux tracés doivent être sur le même graphique.

Je ne vois pas comment déterminer le polynôme sans connaitre les points y.

A bientôt

[GaBuZoMeu]

Il y a mauvaise compréhension.

Que veut dire pour toi interpoler polynomialement la fonction avec comme points d'interpolation, si ce n'est trouver un polynôme de degré tel que pour .
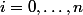
Autrement dit, tes sont bien évidemment les !
Comme je l'ai écrit, il est un peu stupide ici de passer par la méthode d'interpolation de Lagrange.

[novicemaths]

Bonjour

Donc, les calculs que j'ai réalisés à mon premier post son correct pour trouver le polynôme.

A bientôt

[GaBuZoMeu]

Oui, tu as correctement calculé les . Tu aurais pu t'éviter deux calculs en remarquant que est paire.

[novicemaths]

Re bonjour

Voici le graphique.



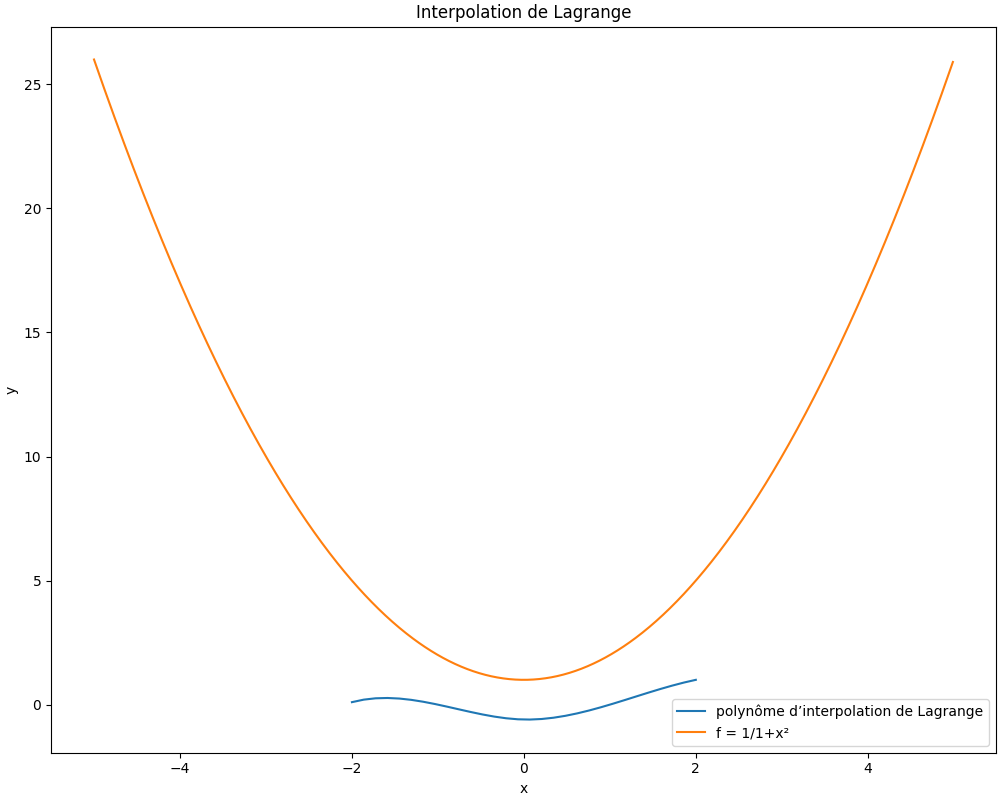
Il me semble que c'est incorrect.

Est-ce que vous confirmez ?

A bientôt

[catamat]

Bonjour
Il semblerait que vous ayez saisi (1/1)+x² au lieu de 1/(1+x²) pour f(x).
Déjà il faut corriger cela.

[novicemaths]

La courbe f est plus belle.

Il faudrait peut-être inversé le polynôme.




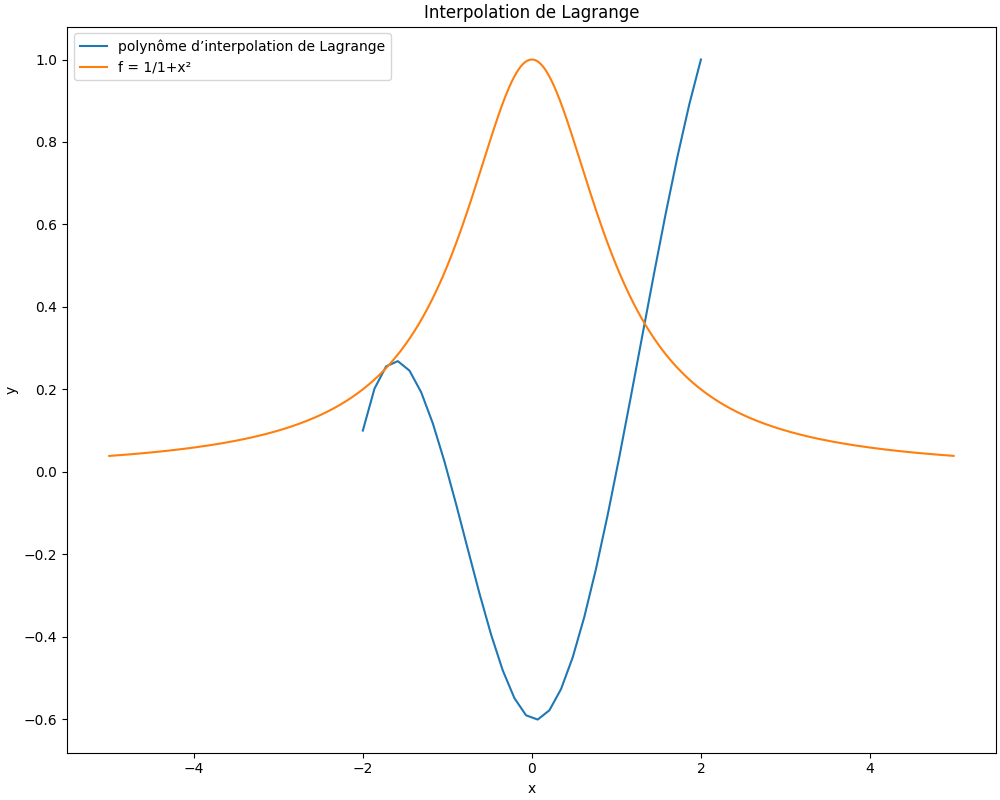
A bientôt

[catamat]

Oui la courbe est correcte mais pas le polynôme.

Comme vous l'a dit GaBuZoMeu il est de la forme car pair et tel que P(0)=1.

et sa représentation graphique passe par A(1,f(1)) et B(2,f(2)) reste à trouver a et b.

[catamat]

Ceci dit on peut aussi trouver le même résultat en utilisant Lagrange, c'est (très)laborieux mais on y arrive...

[catamat]

Le polynôme de Lagrange est une somme ici de 5 polynômes (autant que de points interpolés)
Pour l'abscisse -2 il se présente ainsi :

Les trois points étant les différentes abscisses sauf -2.
On obtient donc :

ou encore


Même chose pour les autres points, pour le développement essayer de faire cela en remarquant certains facteurs communs ce qui permet d'alléger le calcul.

[catamat]

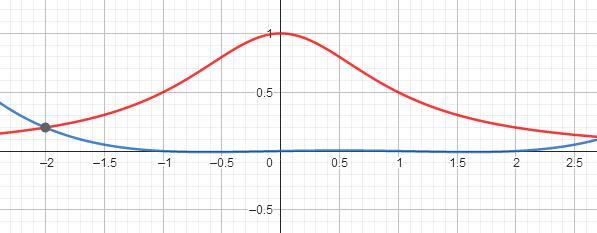
Une remarque : cette fonction polynôme (voir figure) passe par le point de la courbe d'abscisse -2 et s'annule pour les autres valeurs -1, 0, 1 et 2.
On peut trouver les autres fonctions assez rapiement en utilisant cette remarque.