Salut,
zikromanti a écrit:Je sais que le problème est de trouver un polynôme qui coïncide avec une telle fonction (f ) tel que sa première dérivée coïncide avec (f').
Bon, déjà, je sais pas si c'est un problème de Langue ou pas (j'espère que oui...), mais d'exprimer le truc de cette façon là,
ça ne va pas du tout du tout.
Il faut évidement préciser (avant) que :
(1) On se donne une fonction f définie
et dérivable sur un certain intervalle [a,b]
(2)
On se donne n+1 points  de l'intervalle [a,b]
de l'intervalle [a,b].
(3) On cherche un polynôme
de degré au plus 2n+1 dont les valeurs
aux points 
ainsi que les valeur de la dérivée
aux points 
soient les mêmes que celles de

.
Et si je me suis fait c.. à préciser clairement le contexte (en particulier les parties soulignées dont aucune n'est mentionnée dans ton texte), c'est pour bien signaler que si tu ne prend pas l'habitude de
toujours préciser
entièrement le "contexte", ben en math., tu va droit dans le mur...
Bon, sinon, c'est de la bète algèbre linéaire : la fonction

, en fait tu en a rien à faire : le problème se résume à trouver un polynôme

tel que, pour tout

\!=\!\alpha_i)
et
\!=\!\beta_i)
où les

, les
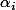
et les
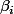
sont fixés d'avance (pour le problème "de base", on prendra
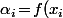)
et
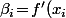)
)
Et évidement, l'algèbre linéaire te dit que résoudre un tel truc et montrer l'unicité de la solution, ça revient à exhiber une base
)
de

telle que, pour tout

, on ait :
(1)
\!=\!0)
pour tout
\!=\!1\ \ \text {et}\ \ Q'_i(x_j)\!=\!0)
pour tout

.
(2)
\!=\!0)
pour tout
\!=\!0)
pour tout
\!=\!1)
.
Et l'unique solution du problème, ça sera bien entendu
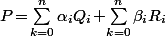
Ensuite, c'est bète comme choux : pour exhiber les polynômes
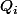
et
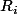
tu utilise le fait que
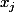
est racine [respectivement racine double] d'un polynôme ssi on peut mettre
)
[respectivement
^2)
] en facteur dans le polynôme en question : tu en déduit en quelques lignes l'expression des
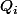
et des